题目内容
在数列{an}中,a1=1,当n≥2时,an-an-1=n,
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)在△ABC中,AB=a3,cosC=
,求△ABC周长的最大值.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)在△ABC中,AB=a3,cosC=
| 1 |
| a2 |
考点:正弦定理
专题:
分析:(Ⅰ)根据已知等式得出an-an-1=n,an-1-an-2=n-1,an-2-an-3=n-2,…,a2-a1=2,左右两边分别相加即可确定出数列{an}的通项公式an;
(Ⅱ)由通项公式an,确定出AB与cosC,利用余弦定理列出关系式,再利用基本不等式求出a+b的最大值,即可确定出三角形ABC周长的最大值.
(Ⅱ)由通项公式an,确定出AB与cosC,利用余弦定理列出关系式,再利用基本不等式求出a+b的最大值,即可确定出三角形ABC周长的最大值.
解答:
解:(Ⅰ)在数列{an}中,a1=1,
an-an-1=n,an-1-an-2=n-1,an-2-an-3=n-2,…,a2-a1=2,
相加得:an-an-1+an-1-an-2+an-2+an-3+…+a2-a1=n+n-1+n-2+…+2,
即an-a1=
-1,
则数列{an}的通项公式an=
;
(Ⅱ)在△ABC中,AB=c=a3=6,cosC=
=
,
∴由余弦定理得:36=a2+b2-2abcosC=a2+b2-
ab=(a+b)2-
ab≥(a+b)2-
×
=
(a+b)2,
整理得:(a+b)2≤108,即a+b≤6
,
则△ABC周长最大值为6+6
.
an-an-1=n,an-1-an-2=n-1,an-2-an-3=n-2,…,a2-a1=2,
相加得:an-an-1+an-1-an-2+an-2+an-3+…+a2-a1=n+n-1+n-2+…+2,
即an-a1=
| n(n+1) |
| 2 |
则数列{an}的通项公式an=
| n(n+1) |
| 2 |
(Ⅱ)在△ABC中,AB=c=a3=6,cosC=
| 1 |
| a2 |
| 1 |
| 3 |
∴由余弦定理得:36=a2+b2-2abcosC=a2+b2-
| 2 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| (a+b)2 |
| 4 |
| 1 |
| 3 |
整理得:(a+b)2≤108,即a+b≤6
| 3 |
则△ABC周长最大值为6+6
| 3 |
点评:此题考查了余弦定理,基本不等式的运用,以及数列的递推,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
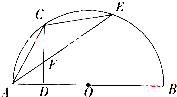 如图,半圆O的直径AB的长为4,点C平分弧AE,过C作AB的垂线交AB于D,交AE干F.
如图,半圆O的直径AB的长为4,点C平分弧AE,过C作AB的垂线交AB于D,交AE干F.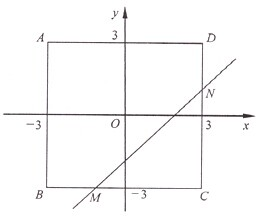 如图,四边形ABCD由不等式组
如图,四边形ABCD由不等式组