题目内容

在椭圆
x2
16
+
y2
12
=1上找一点，使这一点到直线x-2y-12=0的距离的最小值．
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：设出点的坐标，利用点到直线的距离公式，结合三角函数的性质，即可得到结论．
解答： 解：设椭圆的参数方程为
x=4cosθ
y=2
3
sinθ
，则
d=
|4cosθ-4
3
sinθ-12|
5
=
4
5
5
|cosθ-
3
sinθ-3|=
4
5
5
|2cos(θ+
θ
3
)-3|
当cos(θ+
π
3
)=1时，dmin=
4
5
5
，此时所求点为（2，-3）．
点评：本题考查点到直线的距离公式，考查三角函数的性质，属于中档题．
练习册系列答案
相关题目
为了调查某大学学生在周日上网的时间，随机对100名男生和100名女生进行了不记名的问卷调查．得到了如下的统计结果；
表1：男生上网时间与频数分布表
上网时间（分钟） [30，40） [40，50） [50，60） [60，70） [70，80]
人 数 5 25 30 25 15
表2：女生上网时间与频数分布表
上网时间 （分钟） [30，40） [40，50） [50，60） [60，70） [70，80]
人数 10 20 40 20 10
（1）若该大学共有女生750人，试估计其中上网时间不少于60分钟的人数；
（2）完成下面的2×2列联表，并回答能否有90%的把握认为“大学生周日上网时间与性别有关”？
表3
上网时间少于60分钟 上网时间不少于60分钟 合计
男生
女生
合计
附：K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)

P（K2≥k0） 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
k0 0.455 0.708 1.323 2.072 2.706 3.84 5.024 6.635 7.879 10.83
已知函数f（x）=lnx-ax+
1-a
x
-1（a∈R）．
（1）当y=f（x）在点（2，f（2））处的切线方程是y=x+ln2时，求a的值．
（2）当y=f（x）的单调递增区间是（1，5）时，求a的取值集合．
已知矩阵A=
3a
0-1
，a∈R，若点P（2，-3）在矩阵A的变换下得到点P′（3，3）．
（1）则求实数a的值；
（2）求矩阵A的特征值及其对应的特征向量．
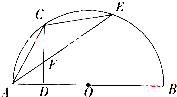如图，半圆O的直径AB的长为4，点C平分弧AE，过C作AB的垂线交AB于D，交AE干F．
（Ⅰ）求证：CE2=AE•AF：
（Ⅱ）若AE是∠CAB的角平分线，求CD的长．
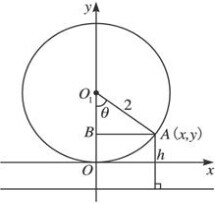如图，某大风车的半径为2米，每12秒旋转一周，它的最低点O离地面0.5米．风车圆周上一点A从最低点O开始，运动t秒后与地面的距离为h米．以O为原点，过点O的圆的切线为x轴，建立直角坐标系．
①假设O1O和O1A的夹角为θ，求θ关于t的关系式；
②当t=4秒时，求扇形OO1A的面积S OO1A；
③求函数h=f（t）的关系式．
设向量
a
=（
3
sinx，sinx），
b
=（cosx，sinx），x∈[0，
π
2
]
（1）若|
a
|=|
b
|，求x的值；
（2）设函数f（x）=
a
•
b
，求f（x）的最大值，并指出对应x的值．
在△ABC中，a，b，c分别是角A，B，C的对边，已知A=60°，B=45°，b=
2
，
（1）求a       
（2）求三角形的面积S．
已知数列{an}是公差不为零的等差数列，a1=1，且a1，a3，a9成等比数列．设数列{2an}的前n项和为Sn，则Sn=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网