题目内容
若双曲线
-
=1的右焦点与抛物线y2=12x的焦点重合,则m= .
| x2 |
| m |
| y2 |
| 4 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出抛物线的焦点,即为双曲线的c=3,再由双曲线的a,b,c的关系,解方程可得m.
解答:
解:抛物线y2=12x的焦点为(3,0),
则双曲线的c=3,
由双曲线
-
=1,可得m+4=9,
解得m=5.
故答案为:5.
则双曲线的c=3,
由双曲线
| x2 |
| m |
| y2 |
| 4 |
解得m=5.
故答案为:5.
点评:本题考查抛物线和双曲线的方程和性质,考查双曲线的a,b,c的关系,考查运算能力,属于基础题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
相关题目
方程log2x+x=0的解所在的区间为( )
A、(0,
| ||
B、(
| ||
| C、(1,2) | ||
| D、[1,2] |
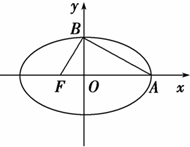 如图,椭圆的中心在坐标原点,F为左焦点,A,B分别为长轴和短轴上的一个顶点,当FB⊥AB时,此类椭圆称为“黄金椭圆”.类比“黄金椭圆”,可推出“黄金双曲线”的离心率为( )
如图,椭圆的中心在坐标原点,F为左焦点,A,B分别为长轴和短轴上的一个顶点,当FB⊥AB时,此类椭圆称为“黄金椭圆”.类比“黄金椭圆”,可推出“黄金双曲线”的离心率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若过定点M(-1,0)且斜率为k的直线与曲线y=
(0<x<1)有交点,则k的取值范围是( )
| 9-(x+2)2 |
A、(0,
| ||
B、(-
| ||
C、(0,
| ||
| D、(0,5) |
已知函数y=f(x)+x是偶函数,且f(2)=3,则f(-2)=( )
| A、-7 | B、7 | C、-5 | D、5 |