题目内容
已知函数g（x）=alnx-x2+ax（a＞0），若y=g（x）在区间（0，2）上不单调，求a的取值范围．
考点：函数单调性的性质
专题：导数的综合应用
分析：求g′（x）=
，所以根据题意知g′（x）在（0，2）上的符号有正有负，结合二次函数图象即可求得a的取值范围．
| -2x2+ax+a |
| x |
解答：
解：g′（x）=
-2x+a=
；
∵g（x）在（0，2）上不单调；
若设f（x）=-2x2+ax+a，则f（x）在（0，2）上有正有负；
∴f（0）f（2）=a（-8+3a）＜0，或
；
解得0＜a＜
；
∴a的取值范围为（0，
）．
| a |
| x |
| -2x2+ax+a |
| x |
∵g（x）在（0，2）上不单调；
若设f（x）=-2x2+ax+a，则f（x）在（0，2）上有正有负；
∴f（0）f（2）=a（-8+3a）＜0，或
|
解得0＜a＜
| 8 |
| 3 |
∴a的取值范围为（0，
| 8 |
| 3 |
点评：考查函数在一区间上不单调时该函数的导数的符号的情况，可结合二次函数图象找限制a的不等式．
练习册系列答案
相关题目
在直三棱柱ABC-A1B1C1中，若
=
，
=
，
=
，则
等于（ ）
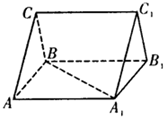
| CA |
| a |
| CB |
| b |
| CC1 |
| c |
| A1B |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
下列判断正确的是（ ）
| A、“b2=ac”是“a，b，c成等比数列”的充分不必要条件 | ||||||||||||
| B、“f（0）=0”是“函数f（x）为奇函数”的必要不充分条件 | ||||||||||||
C、给定向量
| ||||||||||||
D、“0＜α＜β＜
|