题目内容
已知数列{an}中,Sn是其前n项和,并且Sn+1=4an+2(n=1,2,…),a1=1
(1)设bn=an+1-2an(n=1,2,…),求证:数列{bn}是等比数列;
(2)求数列{an}的通项公式;
(3)数列{an}中是否存在最大项与最小项,若存在,求出最大项与最小项;若不存在,说明理由.
(1)设bn=an+1-2an(n=1,2,…),求证:数列{bn}是等比数列;
(2)求数列{an}的通项公式;
(3)数列{an}中是否存在最大项与最小项,若存在,求出最大项与最小项;若不存在,说明理由.
考点:等比关系的确定,数列的函数特性
专题:等差数列与等比数列
分析:(1)利用递推公式可把已知条件进行转化为an+1=4an-2an-1,从而可得数列{bn}为等比数列,
(2)由(1)可得bn=an+1-2an=3•2n-1,构造数列{
},利用数列{
}是等差数列即可求出数列{an}的通项公式.
(3)数列{an}的通项公式的特点,即可得到结论.
(2)由(1)可得bn=an+1-2an=3•2n-1,构造数列{
| an |
| 2n |
| an |
| 2n |
(3)数列{an}的通项公式的特点,即可得到结论.
解答:
解:(1)∵Sn+1=Sn+an+1=4an-1+2+an+1,
∴4an+2=4an-1+2+an+1.
∴an+1-2an=2(an-2an-1)
即bn=2bn-1,且b1=a2-2a1=3,
∴{bn}是公比q=2的等比数列.
(2)∵{bn}是公比q=2的等比数列.
∴bn=3•2n-1,
即bn=an+1-2an=3•2n-1,
∴
-
=
,
即
-
=
,
即{
}是公差d=
,首项
=
的等差数列,
∴
=
+
(n-1),
即an=(3n-1)?2n-2,n≥1.
(3)∵an=(3n-1)?2n-2,n≥1.
∴a1=2?2-1=1,a2=5?20=5,
当n>2时,数列an=(3n-1)?2n-2单调递增,
∴数列{an}存在最小项a1=1,不存在最大项.
∴4an+2=4an-1+2+an+1.
∴an+1-2an=2(an-2an-1)
即bn=2bn-1,且b1=a2-2a1=3,
∴{bn}是公比q=2的等比数列.
(2)∵{bn}是公比q=2的等比数列.
∴bn=3•2n-1,
即bn=an+1-2an=3•2n-1,
∴
| an+1 |
| 2n+1 |
| 2an |
| 2n+1 |
| 3?2n-1 |
| 2n+1 |
即
| an+1 |
| 2n+1 |
| an |
| 2n |
| 3 |
| 4 |
即{
| an |
| 2n |
| 3 |
| 4 |
| a1 |
| 2 |
| 1 |
| 2 |
∴
| an |
| 2n |
| 1 |
| 2 |
| 3 |
| 4 |
即an=(3n-1)?2n-2,n≥1.
(3)∵an=(3n-1)?2n-2,n≥1.
∴a1=2?2-1=1,a2=5?20=5,
当n>2时,数列an=(3n-1)?2n-2单调递增,
∴数列{an}存在最小项a1=1,不存在最大项.
点评:本题主要考查了利用递推公式转化“和”与“项”进而求数列的通项公式,采用构造证明等差(等比数列)也是数列中的重点,要注意掌握运用.

练习册系列答案
相关题目
 读如图的程序:上面的程序如果在执行的时候,输入93,那么输出的结果为( )
读如图的程序:上面的程序如果在执行的时候,输入93,那么输出的结果为( )| A、99 | B、39 |
| C、39.3 | D、99.3 |
如果直线L过点P(3,-1),且与直线x+2y=0垂直,则直线L的方程为( )
| A、x-2y-5=0 |
| B、x+2y-5=0 |
| C、2x-y-7=0 |
| D、2x+y+7=0 |
一个圆柱的侧面展开图是一个正方形,则这个圆柱的底面直径与高的比是( )
A、
| ||
B、
| ||
| C、1 | ||
| D、π |
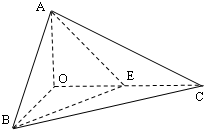 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点. 空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.PM2.5的浓度与空气质量类别的关系如下表所示:
空气质量指数PM2.5(单位:μg/m3)表示每立方米空气中可入肺颗粒物的含量,这个值越高,代表空气污染越严重.PM2.5的浓度与空气质量类别的关系如下表所示: