题目内容
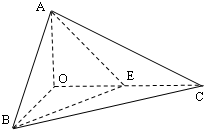 如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
如图,已知三棱锥O-ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.(1)求异面直线EB与AC所成角的余弦值;
(2)求直线EB和平面ABC的所成角的正弦值.
(3)求点E到面ABC的距离.
考点:直线与平面所成的角,异面直线及其所成的角,点、线、面间的距离计算
专题:空间位置关系与距离,空间角
分析:(1)建立空间直角坐标系,求出
=(2,-1,0),
=(0,2,-1),利用计算cos<
,
>,可得异面直线EB与AC所成角的余弦值;
(2)求出平面ABC的法向量,利用向量的夹角公式,即可求直线EB和平面ABC的所成角的正弦值.
(3)利用E点到面ABC的距离d=
=
=
,即可求点E到面ABC的距离.
| EB |
| AC |
| EB |
| AC |
(2)求出平面ABC的法向量,利用向量的夹角公式,即可求直线EB和平面ABC的所成角的正弦值.
(3)利用E点到面ABC的距离d=
|
| ||||
|
|
| 1 | ||
|
| ||
| 6 |
解答:
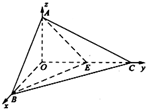 解:(1)以O为原点,OB、OC、OA分别为x、y、z轴建立空间直角坐标系.则有A(0,0,1)、B(2,0,0)、C(0,2,0)、E(0,1,0)…(3分)
解:(1)以O为原点,OB、OC、OA分别为x、y、z轴建立空间直角坐标系.则有A(0,0,1)、B(2,0,0)、C(0,2,0)、E(0,1,0)…(3分)
∴
=(2,-1,0),
=(0,2,-1)
∴cos<
,
>=
=-
…(4分)
∴异面直线EB与AC所成角的余弦值为
…(5分)
(2)设平面ABC的法向量为
=(x,y,z),则
,∴可取
=(1,1,2),…(7分)
∴cos<
,
>=
=
,…(8分)
故BE和平面ABC的所成角的正弦值为
…(9分)
(3)E点到面ABC的距离d=
=
=
∴E点到面ABC的距离为
…(12分)
 解:(1)以O为原点,OB、OC、OA分别为x、y、z轴建立空间直角坐标系.则有A(0,0,1)、B(2,0,0)、C(0,2,0)、E(0,1,0)…(3分)
解:(1)以O为原点,OB、OC、OA分别为x、y、z轴建立空间直角坐标系.则有A(0,0,1)、B(2,0,0)、C(0,2,0)、E(0,1,0)…(3分)∴
| EB |
| AC |
∴cos<
| EB |
| AC |
| -2 | ||||
|
| 2 |
| 5 |
∴异面直线EB与AC所成角的余弦值为
| 2 |
| 5 |
(2)设平面ABC的法向量为
| n1 |
|
| n1 |
∴cos<
| EB |
| n1 |
| 2-1+0 | ||||
|
| ||
| 30 |
故BE和平面ABC的所成角的正弦值为
| ||
| 30 |
(3)E点到面ABC的距离d=
|
| ||||
|
|
| 1 | ||
|
| ||
| 6 |
∴E点到面ABC的距离为
| ||
| 6 |
点评:本题考查向量知识的运用,考查异面直线所成角,线面角,考查点到面的距离,正确运用公式是关键.

练习册系列答案
相关题目
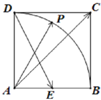 如图所示,在正方形ABCD中,E为AB的中点,P是以A为圆心,AB为半径的圆弧BD上的任意一点,设∠PAB=θ,向量
如图所示,在正方形ABCD中,E为AB的中点,P是以A为圆心,AB为半径的圆弧BD上的任意一点,设∠PAB=θ,向量



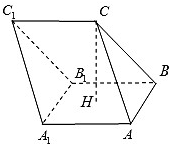 如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2,CH⊥平面AA1B1B,且CH=3.
如图,在三棱柱ABC-A1B1C1中,H是正方形AA1B1B的中心,AA1=2,CH⊥平面AA1B1B,且CH=3.