题目内容
直线y=kx+1与以A(3,2)、B(-2,3)为端点的线段有公共点,则实数k的取值范围是 .
考点:直线的斜率
专题:直线与圆
分析:如图所示,由直线l:y=kx+1,可知直线l过定点P(0,1).利用斜率计算公式可得:kPA,kPB.由于直线y=kx+1与以A(3,2)、B(-2,3)为端点的线段有公共点,可得k≥kPA或k≤kPB,即可得出.
解答:
解:如图所示,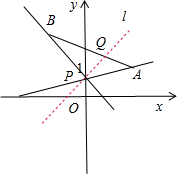
由直线l:y=kx+1,可知直线l过定点P(0,1).
∴kPA=
=
,kPB=
=-1.
∵直线y=kx+1与以A(3,2)、B(-2,3)为端点的线段有公共点,
∴k≥kPA或k≤kPB,
即k≥
或k≤-1.
∴实数k的取值范围是(-∞,-1]∪[
,+∞).
故答案为:(-∞,-1]∪[
,+∞).

由直线l:y=kx+1,可知直线l过定点P(0,1).
∴kPA=
| 2-1 |
| 3-0 |
| 1 |
| 3 |
| 3-1 |
| -2-0 |
∵直线y=kx+1与以A(3,2)、B(-2,3)为端点的线段有公共点,
∴k≥kPA或k≤kPB,
即k≥
| 1 |
| 3 |
∴实数k的取值范围是(-∞,-1]∪[
| 1 |
| 3 |
故答案为:(-∞,-1]∪[
| 1 |
| 3 |
点评:本题考查了直线的斜率与倾斜角的关系、斜率的单调性及计算公式,属于基础题.

练习册系列答案
相关题目
已知曲线y=
x3+
x2+4x-7在点Q处的切线的倾斜角α满足sin2α=
,则此切线的方程为( )
| 1 |
| 3 |
| 1 |
| 2 |
| 16 |
| 17 |
A、4x-y+7=0或4x-y-6
| ||
B、4x-y-6
| ||
C、4x-y-7=0或4x-y-6
| ||
| D、4x-y-7=0 |
圆锥的底面周长为4π,侧面积为8π,则圆锥的母线长为( )
| A、4 | B、3 | C、2 | D、1 |
 如图,正三棱柱ABC-A1B1C1的底面边长为a,当正视图的视线方向垂直于平面AA1B1B时,正视图的面积为2a2,则此时左视图的面积为
如图,正三棱柱ABC-A1B1C1的底面边长为a,当正视图的视线方向垂直于平面AA1B1B时,正视图的面积为2a2,则此时左视图的面积为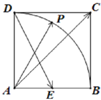 如图所示,在正方形ABCD中,E为AB的中点,P是以A为圆心,AB为半径的圆弧BD上的任意一点,设∠PAB=θ,向量
如图所示,在正方形ABCD中,E为AB的中点,P是以A为圆心,AB为半径的圆弧BD上的任意一点,设∠PAB=θ,向量