题目内容
 以墙为一边,用篱笆围成长方形的场地,并用平行于一边的篱笆隔开(如图),
以墙为一边,用篱笆围成长方形的场地,并用平行于一边的篱笆隔开(如图),已知篱笆总长为50米,写出以边长x表示场地面积y的函数关系式,并求出
函数的定义域及面积的最大值.
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:由题意可知,另一边长为50-3x,则由题意可得y=x(50-3x).由实际情况,可知
,由此求得函数的定义域,再利用二次函数的性质求得y的最大值.
|
解答:
解:由题意可知,另一边长为50-3x,则由题意可得y=x(50-3x)=-3(x-
)2+
,
由实际情况,可知
,解得0<x<
,
∴函数的定义域为(0,
).
∵
∈(0,
),
∴当x=
米时,函数y取得最大值为
平方米.
| 25 |
| 3 |
| 625 |
| 3 |
由实际情况,可知
|
| 50 |
| 3 |
∴函数的定义域为(0,
| 50 |
| 3 |
∵
| 25 |
| 3 |
| 50 |
| 3 |
∴当x=
| 25 |
| 3 |
| 625 |
| 3 |
点评:本题主要考查二次函数的性质的应用,属于中档题.

练习册系列答案
相关题目
已知空间4个球,它们的半径均为2,每个球都与其他三个球外切,另有一个小球与这4个球都外切,则这个小球的半径为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
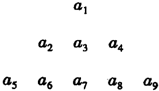 已知数列{an}的通项公式为an=2n(n∈N*),把数列{an}的各项排列成如图所示的三角形数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( )
已知数列{an}的通项公式为an=2n(n∈N*),把数列{an}的各项排列成如图所示的三角形数阵:记M(s,t)表示该数阵中第s行的第t个数,则数阵中的偶数2010对应于( )| A、M(45,15) |
| B、M(45,25) |
| C、M(46,16) |
| D、M(46,25) |
一袋中装有5只球,编号为1,2,3,4,5,在袋中同时取3只,以ξ表示取出的三只球中的最小号码,则P(ξ=2)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
| lim |
| △x→0 |
| f(x0+△x)-f(x0) |
| △x |
| A、恒取正值或恒取负值 |
| B、有时可以取0 |
| C、恒取正值 |
| D、可以取正值和负值,但不能取0 |
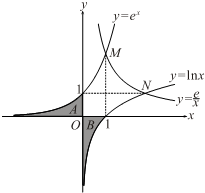 利用自然对数的底数e(e=2.71828…)构建三个基本初等函数
利用自然对数的底数e(e=2.71828…)构建三个基本初等函数