题目内容
已知函数f(x)=
,若f(x0)=-
,则x0= .
|
| 1 |
| 2 |
考点:三角函数的化简求值
专题:三角函数的求值
分析:利用分段函数所给解析式,建立方程,即可求出x0的值.
解答:
解:∵函数f(x)=
,f(x0)=-
,
∴0≤x0≤
时,-sinx0=-
,
∴x0=
;
x0<0时,3x0+
=-
,
∴x0=-
.
故答案为:-
或
.
|
| 1 |
| 2 |
∴0≤x0≤
| π |
| 2 |
| 1 |
| 2 |
∴x0=
| π |
| 6 |
x0<0时,3x0+
| 1 |
| 2 |
| 1 |
| 2 |
∴x0=-
| 1 |
| 3 |
故答案为:-
| 1 |
| 3 |
| π |
| 6 |
点评:本题考查分段函数,考查学生的计算能力,正确运用解析式是关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为V1.直径为4的球的体积为V2,则V1:V2=( )
已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为V1.直径为4的球的体积为V2,则V1:V2=( )| A、1:4 | B、1:2 |
| C、1:1 | D、2:1 |
已知空间4个球,它们的半径均为2,每个球都与其他三个球外切,另有一个小球与这4个球都外切,则这个小球的半径为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
一袋中装有5只球,编号为1,2,3,4,5,在袋中同时取3只,以ξ表示取出的三只球中的最小号码,则P(ξ=2)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
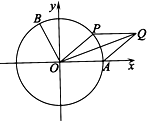 如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B,P在单位圆上,且
如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B,P在单位圆上,且