题目内容
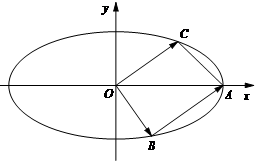 如图,已知椭圆
如图,已知椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(1)求椭圆的方程;
(2)若点B,C(C在第一象限)都在椭圆上,满足
| OC |
| BA |
| OC |
| OB |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由已知条件推导出a=2,
+
=1,由此能求出椭圆的方程.
(2)设直线OC的斜率为k,则直线OC方程为y=kx,直线AB方程为y=k(x-2),分别代入椭圆方程x2+4y2=4,由
•
=0,求出k=
,再由
=λ
,能求出实数λ的值.
| 4e2 |
| a2 |
| ||
| b2 |
(2)设直线OC的斜率为k,则直线OC方程为y=kx,直线AB方程为y=k(x-2),分别代入椭圆方程x2+4y2=4,由
| OC |
| OB |
| ||
| 2 |
| OC |
| BA |
解答:
解:(1)∵椭圆
+
=1 (a>b>0)的右顶点为A(2,0),∴a=2,
∵点P(2e,
)在椭圆上,
∴
+
=1,
∵a2=4,e2=
,a2=b2+c2,
∴b2=1,c2=3,
∴椭圆的方程为
+y2=1.
(2)设直线OC的斜率为k,则直线OC方程为y=kx,
代入椭圆方程
+y2=1,即x2+4y2=4,
得(1+4k2)x2=4,∴xc=
,
∴C(
,
),
又直线AB方程为y=k(x-2),代入椭圆方程x2+4y2=4,
得(1+4k2)x2-16k2x+16k2-4=0,
∵xA=2,∴xB=
,
∵
•
=0,
∴
•
+
•
=0,
∴k2=
,∵C在第一象限,∴k>0,∴k=
,
∵
=(
,
),
=(2-
,0-
)=(
,
),
由
=λ
,得λ=
,
∴k=
,∴λ=
.
| x2 |
| a2 |
| y2 |
| b2 |
∵点P(2e,
| 1 |
| 2 |
∴
| 4e2 |
| a2 |
| ||
| b2 |
∵a2=4,e2=
| c2 |
| 4 |
∴b2=1,c2=3,
∴椭圆的方程为
| x2 |
| 4 |
(2)设直线OC的斜率为k,则直线OC方程为y=kx,
代入椭圆方程
| x2 |
| 4 |
得(1+4k2)x2=4,∴xc=
| 2 | ||
|
∴C(
| 2 | ||
|
| 2k | ||
|
又直线AB方程为y=k(x-2),代入椭圆方程x2+4y2=4,
得(1+4k2)x2-16k2x+16k2-4=0,
∵xA=2,∴xB=
| 2(4k2-1) |
| 1+4k2 |
∵
| OC |
| OB |
∴
| 2(4k2-1) |
| 1+4k2 |
| 2 | ||
|
| -4k |
| 1+4k2 |
| 2k | ||
|
∴k2=
| 1 |
| 2 |
| ||
| 2 |
∵
| OC |
| 2 | ||
|
| 2k | ||
|
| BA |
| 2(4k2-1) |
| 1+4k2 |
| -4k |
| 1+4k2 |
| 4 |
| 1+4k2 |
| 4k |
| 1+4k2 |
由
| OC |
| BA |
k2+
|
∴k=
| ||
| 2 |
| ||
| 2 |
点评:本题考查椭圆方程的求法,考查实数的值的求法,解题时要认真审题,仔细运算,注意推理论证能力的培养.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
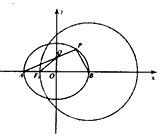 如图,点A,B分别是椭圆E:
如图,点A,B分别是椭圆E: