题目内容
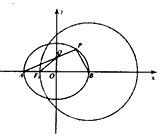 如图,点A,B分别是椭圆E:
如图,点A,B分别是椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)求椭圆E的方程;
(Ⅱ)过A作直线l与y轴交于点Q,与椭圆E交于点P(异于A).
(i)求
| F1Q |
| BP |
(ii)是否存在定圆r,使得以P为圆心,PF1为半径的圆始终内切于圆r,若存在,求出圆r的方程;若不存在,说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出a=2,b2=4-1=3,由此能求出椭圆E.
(Ⅱ)(i)当直线为x轴时,
•
=0.设直线AP:x=ty-2,与E:
+
=1联立,得(3t2+4)y2-12ty=0,由此能求出
•
的取值范围.
(ii)假设存在定圆r满足题意,根据椭圆的对称性,猜想定圆r的圆心在x轴上,由此能求出定圆r的方程.
(Ⅱ)(i)当直线为x轴时,
| F1Q |
| BP |
| x2 |
| 4 |
| y2 |
| 3 |
| F1Q |
| BP |
(ii)假设存在定圆r满足题意,根据椭圆的对称性,猜想定圆r的圆心在x轴上,由此能求出定圆r的方程.
解答:
解:(Ⅰ)依题意知a=2,圆B:(x-2)2+y2=9中,
令y=0,得F1(-1,0),
∴b2=4-1=3,
∴椭圆E:
+
=1.
(Ⅱ)(i)当直线为x轴时,
•
=0.
设直线AP:x=ty-2,与E:
+
=1联立,得(3t2+4)y2-12ty=0,
∴yp=
,xp=
,
AP:x=ty-2中,令x=0,得yp=
,
∴
•
=(1,
)•(
-2,
)=
∈(0,2),
综上所述,
•
的取值范围是[0,2).
(ii)假设存在定圆r满足题意,
根据椭圆的对称性,猜想定圆r的圆心在x轴上,
当P恰好为B时,圆P就是定圆B:(x-2)2+y2=9,交x轴于D(5,0),
当P无限接近于A时,圆P就是圆A:(x+2)2+y2=1,交x轴于C(-3,0).
∴定圆r的圆心为CD中点F2(1,0),恰好为E:
+
=1的右焦点,
∴猜想定圆r:(x-1)2+y2=16.
下证:圆P始终内切于定圆r,
∵|PF2|+|PF1|=4,∴|PF2|=4-|PF1|得证.
令y=0,得F1(-1,0),
∴b2=4-1=3,
∴椭圆E:
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)(i)当直线为x轴时,
| F1Q |
| BP |
设直线AP:x=ty-2,与E:
| x2 |
| 4 |
| y2 |
| 3 |
∴yp=
| 12t |
| 3t2+4 |
| 6t2-8 |
| 3t2+4 |
AP:x=ty-2中,令x=0,得yp=
| 2 |
| t |
∴
| F1Q |
| BP |
| 2 |
| t |
| 6t2-8 |
| 3t2+4 |
| 12t |
| 3t2+4 |
| 8 |
| 3t2+4 |
综上所述,
| F1Q |
| BP |
(ii)假设存在定圆r满足题意,
根据椭圆的对称性,猜想定圆r的圆心在x轴上,
当P恰好为B时,圆P就是定圆B:(x-2)2+y2=9,交x轴于D(5,0),
当P无限接近于A时,圆P就是圆A:(x+2)2+y2=1,交x轴于C(-3,0).
∴定圆r的圆心为CD中点F2(1,0),恰好为E:
| x2 |
| 4 |
| y2 |
| 3 |
∴猜想定圆r:(x-1)2+y2=16.
下证:圆P始终内切于定圆r,
∵|PF2|+|PF1|=4,∴|PF2|=4-|PF1|得证.
点评:本题考查椭圆的几何性质、直线与椭圆的位置关系、圆与圆的位置等基础知识,考查运算求解能力、推理论证能力、探索求解能力;考查数形结合思想、函数与方程、分类与整合等数学思想.

练习册系列答案
相关题目
若点(x,y)在曲线y=-|x|与y=-2所围成的封闭区域内(包括边界),则2x-y的最大值为( )
| A、-6 | B、4 | C、6 | D、8 |
 如图,已知椭圆
如图,已知椭圆