题目内容
抛物线C1:y2=4x的焦点与椭圆C2:
+
=1(a>b>0)的一个焦点相同.设椭圆的右顶点为A,C1,C2在第一象限的交点为B,O为坐标原点,且△OAB的面积为
a.
(1)求椭圆C2的标准方程;
(2)过A点作直线l交C1于C,D两点,连接OC,OD分别交C2于E,F两点,记△OEF,△OCD的面积分别为S1,S2.问是否存在上述直线l使得S2=3S1,若存在,求直线l的方程;若不存在,请说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
(1)求椭圆C2的标准方程;
(2)过A点作直线l交C1于C,D两点,连接OC,OD分别交C2于E,F两点,记△OEF,△OCD的面积分别为S1,S2.问是否存在上述直线l使得S2=3S1,若存在,求直线l的方程;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)由已知条件求出a2=1+b2,yB=
,从而得到B(
,
).再由B点在椭圆上,能求出椭圆C2的标准方程.
(2)设直线l的方程为x=my+2,由
,得y2-4my-8=0,设C(x1,y1),D(x2,y2),由已知条件推导出(
)2=
=
,由48m2=-40,得到不存在直线l使得S2=3S1.
| ||
| 3 |
| 2 |
| 3 |
2
| ||
| 3 |
(2)设直线l的方程为x=my+2,由
|
| S2 |
| S1 |
| ||||
|
| 121+48m2 |
| 32 |
解答:
解:(1)∵y2=4x,∴焦点F(1,0),
∴c=1,即a2=1+b2…(1分)
又∵S△OAB=
×|OA|×yB=
a,∴yB=
…(2分)
代入抛物线方程得B(
,
).
又B点在椭圆上,解得b2=3,a2=4,
∴椭圆C2的标准方程为
+
=1.…(4分)
(2)设直线l的方程为x=my+2,
由
,得y2-4my-8=0,
设C(x1,y1),D(x2,y2),
∴y1+y2=4m,y1•y2=-8…(6分)
又∵
=
=
=|
|×|
|,
直线OC的斜率为
=
,
∴直线OC的方程为x=
,
由
,得
=
,
同理
=
,
∴
=(
)×(
)=
,
则(
)2=
=
,…(10分)
∴
=9,
∴48m2=-40,不成立.
故不存在直线l使得S2=3S1…(12分)
∴c=1,即a2=1+b2…(1分)
又∵S△OAB=
| 1 |
| 2 |
| ||
| 3 |
2
| ||
| 3 |
代入抛物线方程得B(
| 2 |
| 3 |
2
| ||
| 3 |
又B点在椭圆上,解得b2=3,a2=4,
∴椭圆C2的标准方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设直线l的方程为x=my+2,
由
|
设C(x1,y1),D(x2,y2),
∴y1+y2=4m,y1•y2=-8…(6分)
又∵
| S2 |
| S1 |
| ||
|
| |OC||OD| |
| |OE||OF| |
| y1 |
| yE |
| y2 |
| yF |
直线OC的斜率为
| y1 |
| x1 |
| 4 |
| y1 |
∴直线OC的方程为x=
| y1y |
| 4 |
由
|
| y | 2 E |
| 3×64 |
| 3y12+64 |
同理
| y | 2 F |
| 3×64 |
| 3y22+64 |
∴
| y | 2 E |
| y | 2 F |
| 3×64 |
| 3y12+64 |
| 3×64 |
| 3y22+64 |
| 64×32 |
| 121+48m2 |
则(
| S2 |
| S1 |
| ||||
|
| 121+48m2 |
| 32 |
∴
| 121+48m2 |
| 32 |
∴48m2=-40,不成立.
故不存在直线l使得S2=3S1…(12分)
点评:本题考查椭圆方程的求法,考查满足条件的直线是否存在的判断,解题时要认真审题,注意挖题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
设x,y满足约束条件
,则z=3x+y的最大值是( )
|
| A、0 | B、4 | C、5 | D、6 |
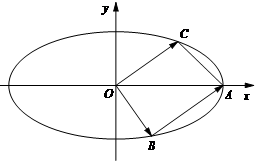 如图,已知椭圆
如图,已知椭圆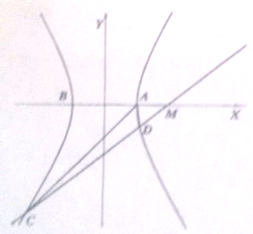 如图所示,已知双曲线
如图所示,已知双曲线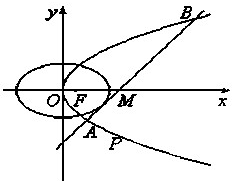 如图所示,已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线l与抛物线C2分别相交于A,B两点.
如图所示,已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线l与抛物线C2分别相交于A,B两点.