题目内容
已知椭圆4x2+y2=1,O是坐标原点.
(Ⅰ)设椭圆在第一象限的部分曲线为C,动点P在C上,C在点P处的切线与x轴、y轴的交点分别为G、H,以OG、OH为邻边作平行四边形OGMH,求点M的轨迹方程;
(Ⅱ)若椭圆与x轴y轴正半轴交于A、B两点,直线y=kx(k>0)与椭圆交于R、S两点,求四边形ARBS面积的最大值.
(Ⅰ)设椭圆在第一象限的部分曲线为C,动点P在C上,C在点P处的切线与x轴、y轴的交点分别为G、H,以OG、OH为邻边作平行四边形OGMH,求点M的轨迹方程;
(Ⅱ)若椭圆与x轴y轴正半轴交于A、B两点,直线y=kx(k>0)与椭圆交于R、S两点,求四边形ARBS面积的最大值.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)曲线C的方程化为y=
,(0<x<
,0<y<1),利用导数的几何意义求出过点P的切线方程,从而求出G点和H点坐标,由四边形OGMH为平行四边形,求出M点坐标,由此能求出点M的轨迹方程.
(Ⅱ)设点R(x1,y1),S(x2,y2),联立
,得(k2+4)x2-1=0,由S四边形ARBS=S△RBS+S△RAS,利用韦达定理和均值定理能求出四边形ARBS面积的最大值.
| 1-4x2 |
| 1 |
| 2 |
(Ⅱ)设点R(x1,y1),S(x2,y2),联立
|
解答:
解:(Ⅰ)由题意,曲线C的方程可化为:
y=
,(0<x<
,0<y<1)
∴y′=
=
,
设曲线C上点P的坐标标为(x0,y0),
则点P处的切线斜率为:
y′|x=x0=
=-
,
∴过点P的切线方程为y-y0=-
(x-x0),
令x=0,得y=y0+
=
,
令y=0,得x=x0+
=
,
∴G(
,0),H(0,
),
设点M从标为(x,y),
∵四边形OGMH为平行四边形,∴
=
+
,
∴
,即
,
又∵点P在椭圆上,∴4(
)2+(
)2=1,
整理,得
+
=1,x>
,y>1,
∴点M的轨迹方程为:
+
=1,x>
,y>1.
(Ⅱ)设点R(x1,y1),S(x2,y2),
联立
,得(kx)2+4x2=1,即(k2+4)x2-1=0,
∴x1+x2=0,x1x2=-
,
由题意知S四边形ARBS=S△RBS+S△RAS
=
(2+k)|x1-x2|
=
(2+k)
=
=
=
≤
=
.
当且仅当k=
(k>0),即k=2时,取“=”号,
∴四边形ARBS面积的最大值为
.
y=
| 1-4x2 |
| 1 |
| 2 |
∴y′=
| -8x | ||
2•
|
| -4x | ||
|
设曲线C上点P的坐标标为(x0,y0),
则点P处的切线斜率为:
y′|x=x0=
| -4x0 | ||
|
| 4x0 |
| y0 |
∴过点P的切线方程为y-y0=-
| 4x0 |
| y0 |
令x=0,得y=y0+
| 4x02 |
| y0 |
| 1 |
| y0 |
令y=0,得x=x0+
| y02 |
| 4x0 |
| 1 |
| 4x0 |
∴G(
| 1 |
| 4x0 |
| 1 |
| y0 |
设点M从标为(x,y),
∵四边形OGMH为平行四边形,∴
| OM |
| OG |
| OH |
∴
|
|
又∵点P在椭圆上,∴4(
| 1 |
| 4x |
| 1 |
| y |
整理,得
| 1 |
| 4x2 |
| 1 |
| y2 |
| 1 |
| 2 |
∴点M的轨迹方程为:
| 1 |
| 4x2 |
| 1 |
| y2 |
| 1 |
| 2 |
(Ⅱ)设点R(x1,y1),S(x2,y2),
联立
|
∴x1+x2=0,x1x2=-
| 1 |
| k2+4 |
由题意知S四边形ARBS=S△RBS+S△RAS
=
| 1 |
| 4 |
=
| 1 |
| 4 |
| (x1+x2)2-4x1x2 |
=
| 1 |
| 4 |
|
=
| 1 |
| 2 |
|
=
| 1 |
| 2 |
1+
|
≤
| 1 |
| 2 |
1+
|
=
| ||
| 2 |
当且仅当k=
| 4 |
| k |
∴四边形ARBS面积的最大值为
| ||
| 2 |
点评:本题考查点的轨迹方程的求法,考查四边形面积最大值的求法,解题时要认真审题,注意均值定理的合理运用.

练习册系列答案
相关题目
已知函数f(x)=x2+bx+c且f(1+x)=f(-x),则下列不等式中成立的是( )
| A、f(-2)<f(0)<f(2) |
| B、f(0)<f(-2)<f(2) |
| C、f(2)<f(0)<f(-2) |
| D、f(0)<f(2)<f(-2) |
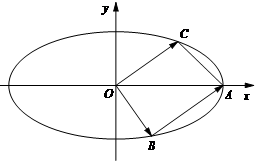 如图,已知椭圆
如图,已知椭圆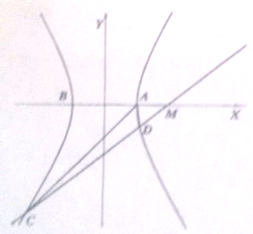 如图所示,已知双曲线
如图所示,已知双曲线 四棱锥P-ABCD的底面是边长为2的菱形,∠DAB=60°,侧棱PA=PC=2
四棱锥P-ABCD的底面是边长为2的菱形,∠DAB=60°,侧棱PA=PC=2