题目内容
计算:
.
| 1+sinx+cosx+2sinxcosx |
| 1+sinx+cosx |
考点:三角函数的化简求值
专题:计算题,三角函数的求值
分析:运用同角的平方关系:1=sin2x+cos2x,分解因式,再由两角和的正弦公式,即可化简.
解答:
解:原式=
=
=
=sinx+cosx=
(
sinx+
cosx)
=
sin(x+
).
| sin2x+cos2x+2sinxcosx+sinx+cosx |
| 1+sinx+cosx |
=
| (sinx+cosx)2+(sinx+cosx) |
| 1+sinx+cosx |
| (sinx+cosx)(sinx+cosx+1) |
| 1+sinx+cosx |
=sinx+cosx=
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| 2 |
| π |
| 4 |
点评:本题考查同角的平方关系和两角和的正弦公式,考查化简整理的运算能力,属于基础题.

练习册系列答案
相关题目
设M=
,N=
,P=
,Q
,则M与N、P与Q的大小关系为( )
| 102012+1 |
| 102013+1 |
| 102013+1 |
| 102014+1 |
| 102012+9 |
| 102013+100 |
| 102013+9 |
| 102014+100 |
| A、M>N,P<Q |
| B、M>N,P<Q |
| C、M>N,P<Q |
| D、M>N,P<Q |
下列说法错误的是( )
| A、在统计里,把所需考察对象的全体叫作总体 |
| B、平均数、众数与中位数从不同的角度描述了一组数据的集中趋势 |
| C、一组数据的平均数一定大于这组数据中的每个数据 |
| D、一组数据的方差越大,说明这组数据的波动越大 |
已知定义在R上的函数f(x)满足f[f(x)]=xf(x)+1,则方程f(x)=0的实根个数为( )
| A、0 | B、1 | C、2 | D、4 |
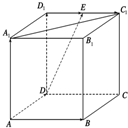 如图所示,在正方体ABCD-A1B1C1D1中,E为D1C1的中点,N为BC的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E为D1C1的中点,N为BC的中点.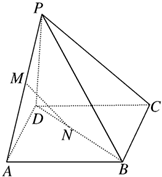 已知正方形ABCD的边长是13,平面ABCD外一点P到正方形各顶点的距离都为13,M、N分别是PA、BD上的点且PM:MA=BN:ND=5:8,如图.
已知正方形ABCD的边长是13,平面ABCD外一点P到正方形各顶点的距离都为13,M、N分别是PA、BD上的点且PM:MA=BN:ND=5:8,如图.