题目内容
给定下列四个命题:其中为真命题的是 (填上正确命题的序号)
①“x=
”是“sinx=
”的充分不必要条件;
②若“p∨q”为真,则“p∧q”为真;
③已知x∈R,则“x>1”是“x>2”的充分不必要条件
④“若am2<bm2,则a<b”的逆命题为真命题.
①“x=
| π |
| 6 |
| 1 |
| 2 |
②若“p∨q”为真,则“p∧q”为真;
③已知x∈R,则“x>1”是“x>2”的充分不必要条件
④“若am2<bm2,则a<b”的逆命题为真命题.
考点:命题的真假判断与应用
专题:简易逻辑
分析:分别根据充分条件和必要条件的定义以及复合命题之间的关系进行判断即可.
解答:
解:①当x=
时,sinx=
成立,即充分性成立,当x=
,满足sinx=
,但x=
不成立,即“x=
”是“sinx=
”的充分不必要条件;故①正确.
②当p真,q假时,满足“p∨q”为真,但“p∧q”为假,故②错误;
③若x=
,满足x>1,但x>2不成立,即“x>1”是“x>2”的充分不必要条件,不成立.故③错误.
④“若am2<bm2,则a<b”的逆命题为:若a<b,则am2<bm2”,当m=0时,为假命题,故④错误.
故真命题为①,
故答案为:①
| π |
| 6 |
| 1 |
| 2 |
| 5π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
②当p真,q假时,满足“p∨q”为真,但“p∧q”为假,故②错误;
③若x=
| 3 |
| 2 |
④“若am2<bm2,则a<b”的逆命题为:若a<b,则am2<bm2”,当m=0时,为假命题,故④错误.
故真命题为①,
故答案为:①
点评:本题主要考查命题的真假判断,要求熟练掌握充分条件和必要条件和复合命题之间的关系.

练习册系列答案
相关题目
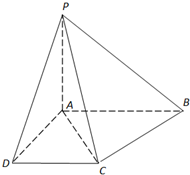 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.