题目内容
正方体ABCD-A1B1C1D1中，M，N分别是CC1，BC的中点，则过A、M、N三点的正方体ABCD-A1B1C1D1的截面形状是（ ）
| A、平行四边形 | B、直角梯形 |
| C、等腰梯形 | D、以上都不对 |
考点：平行投影及平行投影作图法
专题：空间位置关系与距离
分析：延长AN，D1C1，相交于H，根据平面的性质即可得到结论．
解答：
解：连结A1N并延长交D1C1的延长线于H，
连结C1H，
∵M是CC1的中点，
∴直线DH经过点M，
连结MN，
则MN∥AD1，
则等腰梯形ANMD1，即为过A、M、N三点的正方体ABCD-A1B1C1D1的截面，
故选：C
连结C1H，
∵M是CC1的中点，
∴直线DH经过点M，
连结MN，
则MN∥AD1，
则等腰梯形ANMD1，即为过A、M、N三点的正方体ABCD-A1B1C1D1的截面，
故选：C
点评：本题主要考查平面的基本性质，利用延长线的确定平面的交线是解决本题的关键．
练习册系列答案
相关题目
命题“?x∈R，使得x2+x+1＜0”的否定是（ ）
| A、?x∈R，均有x2+x+1＜0 |
| B、?x∈R，均有x2+x+1≥0 |
| C、?x∈R，使得 x2+x+1＜0 |
| D、?x∈R，均有x2+x+1＜0 |
如图，在正方体ABCD-A1B1C1D1中，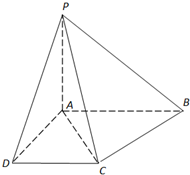
如图，已知四棱锥P-ABCD中，底面ABCD是直角梯形，AB∥DC，∠ABC=45°，DC=1，AB=2，PA⊥平面ABCD，PA=1．