题目内容
13．定义在（0，+∞）上的函数f（x）满足：f（x）＞xf′（x），且f（2）=4，则不等式f（x）-2x＞0的解集为（ ）| A． | （2，+∞） | B． | （0，2） | C． | （0，4） | D． | （4，+∞） |
分析 构造函数g（x）=$\frac{f（x）}{x}$，求函数的导数，利用函数的单调性即可求不等式．
解答 解：设g（x）=$\frac{f（x）}{x}$，
则g′（x）=$\frac{xf′（x）-f（x）}{{x}^{2}}$，
∵f（x）＞xf′（x），
∴g′（x）＜0
即当x＞0时，函数g（x）单调递减，
∵f（2）=4，
∴g（2）=$\frac{f（2）}{2}$=2，
则不等式f（x）-2x＞0等价为g（x）＞g（2），
即0＜x＜2，
则不等式f（x）-2x＞0的解集为（0，2）．
故选：B．
点评 本题主要考查不等式的解法，利用条件构造函数，利用导数研究函数的单调性是解决本题的关键．
练习册系列答案
相关题目
4．中心为原点，一个焦点为$F（0，5\sqrt{2}）$的椭圆截直线y=3x-2所得的弦的中点的横坐标为$\frac{1}{2}$，则椭圆的方程为（ ）
| A． | $\frac{x^2}{25}+\frac{y^2}{75}=1$ | B． | $\frac{x^2}{75}+\frac{y^2}{25}=1$ | C． | $\frac{{2{x^2}}}{75}+\frac{{2{y^2}}}{25}=1$ | D． | $\frac{{2{x^2}}}{25}+\frac{{2{y^2}}}{75}=1$ |
1．已知命题p：?x∈（0，$\frac{π}{2}$），使得cosx≥x，则该命题的否定是（ ）
| A． | ?x∈（0，$\frac{π}{2}$），使得cos x＞x | B． | ?x∈（0，$\frac{π}{2}$），使得cos x≥x | ||
| C． | ?x∈（0，$\frac{π}{2}$），使得cos x＜x | D． | ?x∈（0，$\frac{π}{2}$），使得cos x＜x |
8．复数z满足$\frac{z}{z-i}=i$，则$\overline z$=（ ）
| A． | $\frac{1+i}{2}$ | B． | $\frac{1-i}{2}$ | C． | 1+i | D． | 1-i |
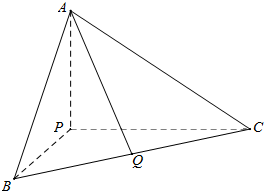在三棱锥P-ABC中，已知PA，PB，PC两两垂直，PB=5，PC=6，三棱锥P-ABC的体积为20，Q是BC的中点，求异面直线PB，AQ所成角的大小（结果用反三角函数值表示）．
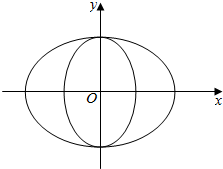如图，曲线Γ由两个椭圆T1：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$和椭圆T2：$\frac{y^2}{b^2}+\frac{x^2}{c^2}=1（{b＞c＞0}）$组成，当a，b，c成等比数列时，称曲线Γ为“猫眼曲线”．