题目内容
8.复数z满足$\frac{z}{z-i}=i$,则$\overline z$=( )| A. | $\frac{1+i}{2}$ | B. | $\frac{1-i}{2}$ | C. | 1+i | D. | 1-i |
分析 把已知等式变形,得到$z=\frac{1}{1-i}$,然后利用复数代数形式的乘除运算化简得答案.
解答 解:由$\frac{z}{z-i}=i$,得z=zi+1,
∴$z=\frac{1}{1-i}=\frac{1+i}{(1-i)(1+i)}=\frac{1+i}{2}$,
则$\overline{z}=\frac{1-i}{2}$.
故选:B.
点评 本题考查复数代数形式的乘除运算,考查共轭复数的概念,是基础的计算题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.定义在(0,+∞)上的函数f(x)满足:f(x)>xf′(x),且f(2)=4,则不等式f(x)-2x>0的解集为( )
| A. | (2,+∞) | B. | (0,2) | C. | (0,4) | D. | (4,+∞) |
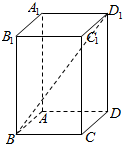 如图,在正四棱柱中ABCD-A1B1C1D1,AB=1,D1B和平面ABCD所成的角的大小为$arctan\frac{{3\sqrt{2}}}{4}$,求该四棱柱的表面积.
如图,在正四棱柱中ABCD-A1B1C1D1,AB=1,D1B和平面ABCD所成的角的大小为$arctan\frac{{3\sqrt{2}}}{4}$,求该四棱柱的表面积.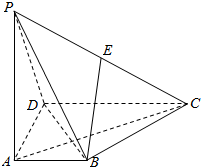 如图,在四棱锥P-ABCD中,PA⊥ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.