题目内容
1.已知命题p:?x∈(0,$\frac{π}{2}$),使得cosx≥x,则该命题的否定是( )| A. | ?x∈(0,$\frac{π}{2}$),使得cos x>x | B. | ?x∈(0,$\frac{π}{2}$),使得cos x≥x | ||
| C. | ?x∈(0,$\frac{π}{2}$),使得cos x<x | D. | ?x∈(0,$\frac{π}{2}$),使得cos x<x |
分析 直接利用特称命题的否定是全称命题写出结果即可.
解答 解:因为特称命题的否定是全称命题,所以,命题p:?x∈(0,$\frac{π}{2}$),使得cosx≥x,则该命题的否定是:?x∈(0,$\frac{π}{2}$),使得cos x<x.
故选:D.
点评 本题考查命题的否定特称命题与全称命题的否定关系,是基础题.

练习册系列答案
相关题目
9.椭圆满足这样的光学性质:从椭圆的一个焦点发射光线,经椭圆反射后,反射光线经过椭圆的另一焦点.现在设有一个水平放置的椭圆形台球盘,满足方程$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1,点A、B是它的两个焦点,当静止的小球放在A处,从点A沿直线出发,经椭圆壁反弹后,再回到点A时,小球经过的路程是( )
| A. | 20 | B. | 18 | C. | 2 | D. | 以上均有可能 |
13.定义在(0,+∞)上的函数f(x)满足:f(x)>xf′(x),且f(2)=4,则不等式f(x)-2x>0的解集为( )
| A. | (2,+∞) | B. | (0,2) | C. | (0,4) | D. | (4,+∞) |
 某高三年级从甲(文)乙(理)两个年级组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩(满分:100分)的茎叶图如图所示,其中甲组学生的平均分是85分,乙组学生成绩的中位数是83分.
某高三年级从甲(文)乙(理)两个年级组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩(满分:100分)的茎叶图如图所示,其中甲组学生的平均分是85分,乙组学生成绩的中位数是83分.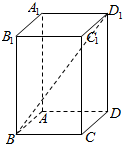 如图,在正四棱柱中ABCD-A1B1C1D1,AB=1,D1B和平面ABCD所成的角的大小为$arctan\frac{{3\sqrt{2}}}{4}$,求该四棱柱的表面积.
如图,在正四棱柱中ABCD-A1B1C1D1,AB=1,D1B和平面ABCD所成的角的大小为$arctan\frac{{3\sqrt{2}}}{4}$,求该四棱柱的表面积.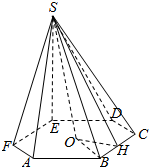 正六棱锥的底面周长为24,斜高SH与高SO所成的角为30°.
正六棱锥的底面周长为24,斜高SH与高SO所成的角为30°.