题目内容
18.已知函数f(x)=xlnx(1)当x≥1时,若f(x)≥a(x-1)恒成立,求a的取值范围;
(2)求证:当n≥2且n∈N*时,$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}<lnn$.
分析 (1)原不等式可化为xlnx≥a(x-1),从而讨论x=1与x>1时不等式成立的条件即可;
(2)根据lnx>$\frac{x-1}{x}$(x>1),令x=$\frac{n}{n-1}$(n≥2且n∈N*),即ln$\frac{n}{n-1}$>$\frac{1}{n}$,通过赋值叠加即可.
解答 解:(1)f(x)≥a(x-1)(x≥1)可化为
xlnx≥a(x-1),
当x=1时,0≥0,显然成立;
当x>1时,不等式可化为a≤$\frac{xlnx}{x-1}$,
令g(x)=$\frac{xlnx}{x-1}$,g′(x)=$\frac{(lnx+1)(x-1)-xlnx}{{(x-1)}^{2}}$=$\frac{x-lnx-1}{{(x-1)}^{2}}$,
令h(x)=x-lnx-1,h′(x)=1-$\frac{1}{x}$,
故h(x)=x-lnx-1在(1,+∞)上是增函数,
故x-lnx-1>1-0-1=0,
故g′(x)=$\frac{x-lnx-1}{{(x-1)}^{2}}$>0;
故g(x)=$\frac{xlnx}{x-1}$在(1,+∞)上是增函数,且 $\underset{lim}{x{→1}^{+}}$$\frac{xlnx}{x-1}$=1,
故a≤1;
(2)当a=1时:lnx>$\frac{x-1}{x}$(x>1),
令x=$\frac{n}{n-1}$(n≥2且n∈N*),即ln$\frac{n}{n-1}$>$\frac{1}{n}$,
得:lnn-ln(n-1)>$\frac{1}{n}$,
∴ln(n-1)-ln(n-2)>$\frac{1}{n-1}$,
ln(n-2)-ln(n-3)>$\frac{1}{n-2}$,
…,
ln2-ln1>$\frac{1}{2}$,
上述各式相加得:lnn>$\frac{1}{n}$+$\frac{1}{n-1}$+…+$\frac{1}{3}$+$\frac{1}{2}$,
即当n≥2且n∈N*时,$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}<lnn$.
点评 本题考查了导数的综合应用及恒成立问题,同时考查了极限的求法.

| A. | 20 | B. | 18 | C. | 2 | D. | 以上均有可能 |
| A. | (2,+∞) | B. | (0,2) | C. | (0,4) | D. | (4,+∞) |
| A. | 过直线a可以作一个平面并且只可以作一个平面α与直线b平行 | |
| B. | 过直线a至多可以作一个平面α与直线b垂直 | |
| C. | 唯一存在一个平面α与直线a、b等距 | |
| D. | 可能存在平面α与直线a、b都垂直 |
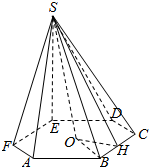 正六棱锥的底面周长为24,斜高SH与高SO所成的角为30°.
正六棱锥的底面周长为24,斜高SH与高SO所成的角为30°.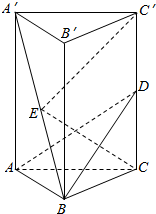 如图,在正三棱柱ABC-A′B′C′中,D、E分别为CC′,A′B中点,CC′=$\sqrt{3}BC$.求证:
如图,在正三棱柱ABC-A′B′C′中,D、E分别为CC′,A′B中点,CC′=$\sqrt{3}BC$.求证: