题目内容
1．若直线l过点A（3，4），且点B（-3，2）到直线l的距离最远，则直线l的方程为（ ）| A． | 3x-y-5=0 | B． | 3x-y+5=0 | C． | 3x+y+13=0 | D． | 3x+y-13=0 |
分析 l⊥AB时满足条件．利用斜率计算公式、点斜式即可得出．
解答 解：l⊥AB时满足条件．
kAB=$\frac{2-4}{-3-3}$=$\frac{1}{3}$，则kl=-3．
∴直线l的方程为：y-4=-3（x-3），化为：3x+y-13=0．
故选：D．
点评 本题考查了相互垂直的直线斜率之间的关系、斜率计算公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
5．已知△ABC中，内角A，B，C的对边分别为a，b，c，若a2=b2+c2-bc，a=4，则△ABC的外接圆半径为（ ）
| A． | $\frac{{4\sqrt{3}}}{3}$ | B． | $\frac{{8\sqrt{3}}}{3}$ | C． | 4 | D． | 8 |
10．已知$\overrightarrow{a}$，$\overrightarrow{b}$为单位向量，且|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{2}$|$\overrightarrow{a}-\overrightarrow{b}$|，则$\overrightarrow{a}$在$\overrightarrow{a}+\overrightarrow{b}$上的投影为（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{2\sqrt{6}}{3}$ | C． | $\frac{\sqrt{6}}{3}$ | D． | $\frac{2\sqrt{2}}{3}$ |
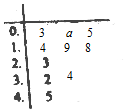已知函数f（x）=x2+$\sqrt{2}$（m-1）x+$\frac{m}{4}$，现有一组数据（该组数据数量庞大），从中随机抽取10个，绘制所得的茎叶图如图所示，且茎叶图中的数据的平均数为2．