题目内容
13.设F1为椭圆C1:$\frac{(x-1)^{2}}{16}+\frac{{y}^{2}}{12}$=1的左焦点,M是C1上任意一点,P是线段F1M的中点;(])求动点P的轨迹C的方程;
(2)若直线y=kx+2交轨迹C于A,B两点,AB的中垂线交y轴于点Q(0,t),求t的范围.
分析 (1)设P(x,y),根据中点坐标公式得出M点坐标,代入椭圆C1方程化简即可得出动点P的轨迹C的方程;
(2)联立方程组,根据根与系数的关系得出AB的中点坐标,由判别式大于零得出k的范围,得出AB的中垂线方程,求得t关于k的表达式,根据k的范围得出t的范围.
解答 解:(1)F1(-1,0),设P(x,y),则M(2x+1,2y),
∵M在椭圆C1:$\frac{(x-1)^{2}}{16}+\frac{{y}^{2}}{12}$=1上,∴$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
即动点P的轨迹C的方程是$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}$=1.
(2)联立方程组$\left\{\begin{array}{l}{y=kx+2}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,消元得(3+4k2)x2+16kx+4=0,
令△=(16k)2-16(3+4k2)>0,解得k$>\frac{1}{2}$或k<-$\frac{1}{2}$.
设A(x1,y1),B(x2,y2),则x1+x2=-$\frac{16k}{3+4{k}^{2}}$,y1+y2=k(x1+x2)+4=$\frac{12}{3+4{k}^{2}}$,
∴AB的中点坐标为(-$\frac{8k}{3+4{k}^{2}}$,$\frac{6}{3+4{k}^{2}}$),
∴AB的中垂线方程为y-$\frac{6}{3+4{k}^{2}}$=-$\frac{1}{k}$(x+$\frac{8k}{3+4{k}^{2}}$),
令x=0得y=$\frac{-2}{3+4{k}^{2}}$,即t=$\frac{-2}{3+4{k}^{2}}$,
∵k2$>\frac{1}{4}$,∴t<-$\frac{1}{2}$.
点评 本题考查了轨迹方程的求解,直线与椭圆的位置关系,属于中档题.

| A. | x<0 | B. | x<0或x>4 | C. | |x-1|>1 | D. | |x-2|>3 |
| A. | 3x-y-5=0 | B. | 3x-y+5=0 | C. | 3x+y+13=0 | D. | 3x+y-13=0 |
| A. | $\frac{4\sqrt{5}}{3}$ | B. | 4$\sqrt{5}$ | C. | $\frac{8\sqrt{5}}{3}$ | D. | 8$\sqrt{5}$ |
| A. | -2 | B. | 2 | C. | -3 | D. | 3 |
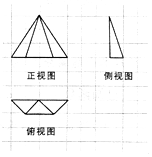
| A. | 3 | B. | 3$\sqrt{2}$ | C. | 9 | D. | 9$\sqrt{2}$ |
| A. | 94 | B. | 96 | C. | 190 | D. | 192 |