题目内容
10.一个几何体的三视图如图所示,则该几何体的体积为4$\sqrt{3}$+1.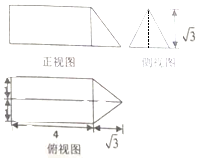
分析 首先根据三视图把平面图转换成立体图形,进一步利用几何体的体积公式求出结果.
解答 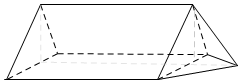 解:根据几何体的三视图可知,该几何体是一个三棱柱和一个三棱锥所组成的,如图所示,
解:根据几何体的三视图可知,该几何体是一个三棱柱和一个三棱锥所组成的,如图所示,
且其底面均为高为$\sqrt{3}$的等边三角形,其面积为$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$,
三棱柱的高为4,三棱锥的高为$\sqrt{3}$,
故几何体的体积为$\sqrt{3}$×4+$\frac{1}{3}$×$\sqrt{3}$×$\sqrt{3}$=4$\sqrt{3}$+1,
故答案为:4$\sqrt{3}$+1
点评 本题考查的知识要点:三视图和立体图之间的转换,几何体的体积公式的应用,主要考查学生的空间想象能力和应用能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.若直线l过点A(3,4),且点B(-3,2)到直线l的距离最远,则直线l的方程为( )
| A. | 3x-y-5=0 | B. | 3x-y+5=0 | C. | 3x+y+13=0 | D. | 3x+y-13=0 |
18.(a+x)(1+x)4的展开式中x的奇数次幂项的系数之和为32,则a=( )
| A. | -2 | B. | 2 | C. | -3 | D. | 3 |
5.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的体积为( )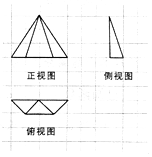

| A. | 3 | B. | 3$\sqrt{2}$ | C. | 9 | D. | 9$\sqrt{2}$ |
15.已知三棱锥S-ABC,△ABC是直角三角形,其斜边AB=8,SC⊥平面ABC,SC=6,则三棱锥的外接球的表面积为( )
| A. | 64π | B. | 68π | C. | 72π | D. | 100π |