题目内容
10.已知$\overrightarrow{a}$,$\overrightarrow{b}$为单位向量,且|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{2}$|$\overrightarrow{a}-\overrightarrow{b}$|,则$\overrightarrow{a}$在$\overrightarrow{a}+\overrightarrow{b}$上的投影为( )| A. | $\frac{1}{3}$ | B. | -$\frac{2\sqrt{6}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{2}}{3}$ |
分析 由已知向量等式求得$\overrightarrow{a}•\overrightarrow{b}$,进一步求出$\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})$,$|\overrightarrow{a}+\overrightarrow{b}|$的值,代入投影表达式计算.
解答 解:由$\overrightarrow{a}$,$\overrightarrow{b}$为单位向量,知$|\overrightarrow{a}|=|\overrightarrow{b}|=1$,
再由且|$\overrightarrow{a}+\overrightarrow{b}$|=$\sqrt{2}$|$\overrightarrow{a}-\overrightarrow{b}$|,得$(\overline{a}+\overline{b})^{2}=2(\overrightarrow{a}-\overrightarrow{b})^{2}$,
即${\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}=2{\overrightarrow{a}}^{2}-4\overrightarrow{a}•\overrightarrow{b}+2{\overrightarrow{b}}^{2}$,
∴$\overrightarrow{a}•\overrightarrow{b}=\frac{1}{3}$.
则$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{(\overrightarrow{a}+\overrightarrow{b})^{2}}=\sqrt{{\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}}$=$\sqrt{1+\frac{2}{3}+1}=\frac{2\sqrt{6}}{3}$.
$\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})={\overrightarrow{a}}^{2}+\overrightarrow{a}•\overrightarrow{b}=1+\frac{1}{3}=\frac{4}{3}$.
∴$\overrightarrow{a}$在$\overrightarrow{a}+\overrightarrow{b}$上的投影为$\frac{\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})}{|\overrightarrow{a}+\overrightarrow{b}|}=\frac{\frac{4}{3}}{\frac{2\sqrt{6}}{3}}=\frac{\sqrt{6}}{3}$.
故选:C.
点评 本题考查平面向量的数量积运算,考查向量在向量方向上投影的概念,是中档题.

| A. | 第一象限 | B. | 第三象限 | C. | 第二象限 | D. | 第四象限 |
| A. | 18 | B. | 24 | C. | 27 | D. | 36 |
| A. | 3x-y-5=0 | B. | 3x-y+5=0 | C. | 3x+y+13=0 | D. | 3x+y-13=0 |
| A. | $\frac{4\sqrt{5}}{3}$ | B. | 4$\sqrt{5}$ | C. | $\frac{8\sqrt{5}}{3}$ | D. | 8$\sqrt{5}$ |
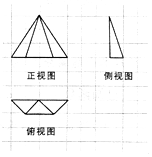
| A. | 3 | B. | 3$\sqrt{2}$ | C. | 9 | D. | 9$\sqrt{2}$ |
| A. | (-∞,1) | B. | (∞,1] | C. | (1,+∞) | D. | [1,+∞) |