题目内容
10.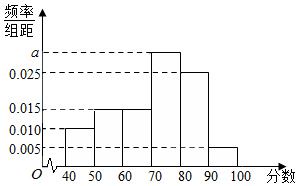 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成如下六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成如下六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.(1)若该校高一年级共有学生640名,试估计该校高一年级期中考试数学成绩不低于60分的人数.
(2)在抽取的40名学生中,若从数学成绩在[40,50)与[90,100]两个分数段内随机选取2名学生,求这2名学生的数学成绩之差的绝对值不大于10的槪率.
分析 (1)由频率分布直方图中频率之和为1,能求出a,由频率分布直方图:成绩不低于60分的频率1-10×(0.05+0.01)=0.85,故估计高一年级期中考试数学成绩不低于60分的人数.
(2)由频率分布直方图,得数学成绩在[40,50)内的学生人数为40×0.05=2,这两人分别记为A,B,数学成绩在[90,100)内的学生人数为40×0.1=4,这4人分别记为C,D,E,F,如果这两名学生的数学成绩都在[40,50)或都在[90,100)内,则这两名学生的数学成绩之差的绝对值不大于10,由此利用列举法能过河卒子同这两名学生的数学成绩之差的绝对值不大于10的概率.
解答 解:(1)由频率分布直方图,得:
10×(0.005+0.01+0.025+a+0.01)=1,
解得a=0.03.
由频率分布直方图:成绩不低于60分的频率1-10×(0.05+0.01)=0.85,
估计期中考试成绩不低于60分的人数为约为640×0.85=544
(2)由频率分布直方图,得数学成绩在[40,50)内的学生人数为40×0.05=2,这两人分别记为A,B,
数学成绩在[90,100)内的学生人数为40×0.1=4,这4人分别记为C,D,E,F,
若从数学成绩在[40,50)与[90,100)两个分数段内的学生中随机选取2名学生,
则所有的基本事件有:
(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),
(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共15个,
如果这两名学生的数学成绩都在[40,50)或都在[90,100)内,
则这两名学生的数学成绩之差的绝对值不大于10,
记“这两名学生的数学成绩之差的绝对值不大于10”为事件M,
则事件M包含的基本事件有:(A,B),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F),共7个,
所以这两名学生的数学成绩之差的绝对值不大于10的概率P=$\frac{7}{15}$.
点评 本题考查频率和概率的求法,解题时要认真审题,注意频率分布直方图和列举法的合理运用,属于中档题.

 全能练考卷系列答案
全能练考卷系列答案| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
| A. | 108 | B. | 120 | C. | 132 | D. | 144 |
| A. | 4 cm | B. | 5cm | C. | 6cm | D. | 7cm |
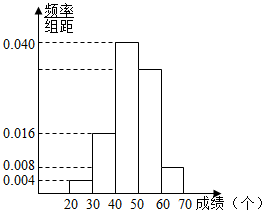 体育课上,李老师对初三 (1)班50名学生进行跳绳测试,现测得他们的成绩(单位:个)全部介于20与70之间,将这些成绩数据进行分组(第一组:(20,30],第二组:(30,40],…,第五组:(60,70]),并绘制成如图所示的频率分布直方图.
体育课上,李老师对初三 (1)班50名学生进行跳绳测试,现测得他们的成绩(单位:个)全部介于20与70之间,将这些成绩数据进行分组(第一组:(20,30],第二组:(30,40],…,第五组:(60,70]),并绘制成如图所示的频率分布直方图.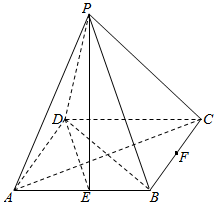 如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上,E,F分别是AB,BC的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上,E,F分别是AB,BC的中点.