题目内容
20.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F(c,0),过F且垂直于x轴的直线在第一象限内与双曲线、双曲线的渐近线的交点依次为A,B,若A为BF的中点,则双曲线的离心率为( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
分析 设出渐近线方程,将x=c分别代入双曲线的方程和渐近线方程,求得交点A,B,再由中点坐标公式和离心率公式,计算即可得到所求值.
解答 解:由题意可得F(c,0),渐近线方程为y=$\frac{b}{a}$x,
将x=c,代入双曲线的方程可得y=±b$\sqrt{\frac{{c}^{2}}{{a}^{2}}-1}$=±$\frac{{b}^{2}}{a}$,
可得A(c,$\frac{{b}^{2}}{a}$);
将x=c代入渐近线方程可得y=$\frac{bc}{a}$,
可得B(c,$\frac{bc}{a}$),
由A为BF的中点,可得$\frac{2{b}^{2}}{a}$=$\frac{bc}{a}$,
化简可得c=2b,
即c2=4b2=4(c2-a2),
即有c=$\frac{2\sqrt{3}}{3}$a,
即e=$\frac{c}{a}$=$\frac{2\sqrt{3}}{3}$.
故选:A.
点评 本题考查双曲线的留下来的求法,注意运用联立直线方程求得交点和中点坐标公式,考查运算能力,属于中档题.

练习册系列答案
相关题目
10.已知函数f(x)=$\left\{\begin{array}{l}{2(x+1)(-1≤x≤0)}\\{2-x(0<x≤2)}\end{array}\right.$,不等式f(x)≤lo${g}_{\frac{1}{2}}$(x+1)的解集是( )
| A. | {x|-1<x≤0} | B. | {x|-1<x≤-$\frac{1}{2}$} | C. | {x|-1≤x≤-$\frac{1}{2}$} | D. | {x|-1≤x≤-$\frac{1}{3}$} |
11.已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的两条渐近线的斜率之积为-2,焦距为6,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | B. | $\frac{x^2}{24}$-$\frac{y^2}{12}$=1 | C. | $\frac{x^2}{3}$-$\frac{y^2}{6}$=1 | D. | $\frac{x^2}{6}$-$\frac{y^2}{3}$=1 |
8.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点为F,点F到渐近线的距离为2a,则该双曲线的离心率等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 3 |
15.据《法制晚报》报道,2009年8月15日至8月28日,全国查处酒后驾车和醉酒驾车共28800人,图1是对这28800人血液中酒精含量进行检测所得结果的频率分布直方图,从左到右各直方块表示的人数依次记为A1、A2、…、A8(例如A2表示血液酒精浓度在30~40mg/100ml的人数),图2是对图1中血液酒精浓度在某一范围内的人数进行统计的程序框图.这个程序框图输出的s=( )
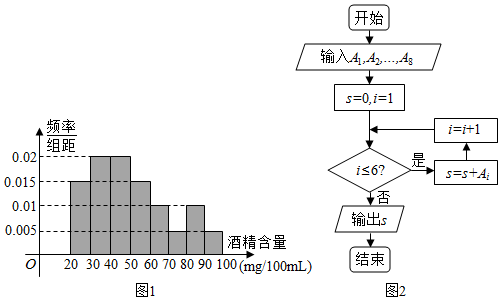

| A. | 24480 | B. | 24380 | C. | 23040 | D. | 23140 |
5.已知复数z满足zi=1-i,(i为虚数单位),则|z|=( )
| A. | 1 | B. | 2 | C. | 3 | D. | $\sqrt{2}$ |
12.命题“有些相互垂直的两直线不相交”的否定是( )
| A. | 有些相互垂直的两直线相交 | B. | 有些不相互垂直的两直线不相交 | ||
| C. | 任意相互垂直的两直线相交 | D. | 任意相互垂直的两直线不相交 |
9.设命题p:函数f(x)=x2+ax+$\frac{1}{x}$在($\frac{1}{2}$,+∞)上是增函数,命题q:a≥0,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
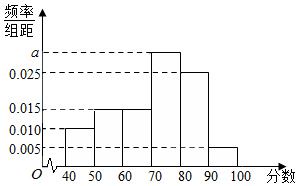 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成如下六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成如下六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.