题目内容
1．2016年某高校艺术类考试中，共有6位选手参加，其中3位女生，3位男生，现这六名考试依次出场进行才艺展出，如果3位男生中任何两人都不能连续出场，且女生甲不能排第一个，那么这六名考生出场顺序的排法种数为（ ）| A． | 108 | B． | 120 | C． | 132 | D． | 144 |
分析 利用间接法，先求出3位男生中任何两人都不能连续出场的种数，再其排除女生甲排第一个的种数，问题得以解决．
解答 解：把3名男生插入到3名女生所成的4个间隔中，故有A33A43=144种，女生甲排第一个，A22A33=12种，
故女生甲不能排第一个，那么这六名考生出场顺序的排法种数为144-12=132种，
故选：C．
点评 本题主要考查排列组合、两个基本原理的应用，注意特殊位置优先排，不相邻问题用插空法，体现了分类讨论的数学思想，属于中档题．
练习册系列答案
相关题目
11．已知双曲线$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0）的两条渐近线的斜率之积为-2，焦距为6，则双曲线的方程为（ ）
| A． | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | B． | $\frac{x^2}{24}$-$\frac{y^2}{12}$=1 | C． | $\frac{x^2}{3}$-$\frac{y^2}{6}$=1 | D． | $\frac{x^2}{6}$-$\frac{y^2}{3}$=1 |
12．命题“有些相互垂直的两直线不相交”的否定是（ ）
| A． | 有些相互垂直的两直线相交 | B． | 有些不相互垂直的两直线不相交 | ||
| C． | 任意相互垂直的两直线相交 | D． | 任意相互垂直的两直线不相交 |
9．设命题p：函数f（x）=x2+ax+$\frac{1}{x}$在（$\frac{1}{2}$，+∞）上是增函数，命题q：a≥0，则p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
16．在△ABC中，a=8，b=7，A=45°，则此三角形解的情况是（ ）
| A． | 一解 | B． | 两解 | C． | 一解或两解 | D． | 无解 |
6．在等比数列{an}中，a3，a15是方程x2-6x+8=0的根，则$\frac{{{a_1}{a_{17}}}}{a_9}$的值为（ ）
| A． | $2\sqrt{2}$ | B． | 4 | C． | $±2\sqrt{2}$ | D． | ±4 |
13．向量$\overrightarrow{O{Z_1}}$对应的复数是5-4i，向量$\overrightarrow{O{Z_2}}$对应的复数是-5+4i，则向量$\overrightarrow{{Z_1}{Z_2}}$对应的复数是（ ）
| A． | -10+8i | B． | 10-8i | C． | -8+10i | D． | 8+-10i |
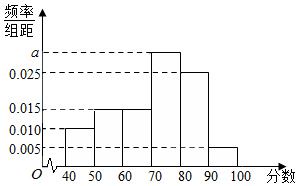某校从高一年级学生中随机抽取40名学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成如下六段：[40，50），[50，60），…，[90，100]后得到如图的频率分布直方图．
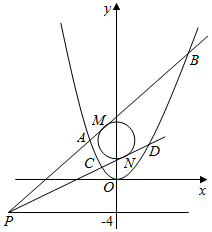在直角坐标系xOy中，抛物线C1：x2=4y和圆C2：x2+（y-5）2=9，点P是直线y=-4上的动点．