题目内容
15.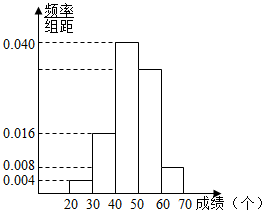 体育课上,李老师对初三 (1)班50名学生进行跳绳测试,现测得他们的成绩(单位:个)全部介于20与70之间,将这些成绩数据进行分组(第一组:(20,30],第二组:(30,40],…,第五组:(60,70]),并绘制成如图所示的频率分布直方图.
体育课上,李老师对初三 (1)班50名学生进行跳绳测试,现测得他们的成绩(单位:个)全部介于20与70之间,将这些成绩数据进行分组(第一组:(20,30],第二组:(30,40],…,第五组:(60,70]),并绘制成如图所示的频率分布直方图.(1)求成绩在第四组的人数和这50名同学跳绳成绩的中位数;
(2)从成绩在第一组和第五组的同学中随机取出 2名同学进行搭档,求至少有一名同学在第一组的概率.
分析 (1)根据频率分步直方图即可求出成绩在第四组的人数,估计中位数即可.
(2)根据频率分步直方图做出要用的各段的人数,设出各段上的元素,用列举法写出所有的事件和满足条件的事件,根据概率公式做出概率.
解答 解:(1)第四组的人数为[1-(0.004+0.008+0.016+0.04)×10]×50=16,
中位数为40+[0.5-(0.004+0.016)×10]÷0.04=47.5.
(2)据题意,第一组有0.004×10×50=2人,第五组有0.008×10×50=4人,
记第一组成绩为A,B,第五组成绩为a,b,c,d,
则可能构成的基本事件有(A,a),(A,b),(A,c),(A,d),(B,a),(B,b),(B,c),(B,d),(A,B),(a,b),(a,c),(a,d),(b,c),(b,d),(c,d)共15种,
其中至少有一名是第一组的有(A,a),(A,b),(A,c),(A,d),(B,a),(B,b),(B,c),(B,d),(A,B),共9种,
∴概率$P=\frac{9}{15}=\frac{3}{5}$.
点评 本题是一个典型的古典概型问题,本题可以列举出试验发生包含的事件和满足条件的事件,应用列举法来解题是这一部分的精髓.

练习册系列答案
相关题目
5.已知复数z满足zi=1-i,(i为虚数单位),则|z|=( )
| A. | 1 | B. | 2 | C. | 3 | D. | $\sqrt{2}$ |
6.在等比数列{an}中,a3,a15是方程x2-6x+8=0的根,则$\frac{{{a_1}{a_{17}}}}{a_9}$的值为( )
| A. | $2\sqrt{2}$ | B. | 4 | C. | $±2\sqrt{2}$ | D. | ±4 |
20.设随机变量X的概率分布表如表,则P(|X-2|=1)=( )
| X | 1 | 2 | 3 | 4 |
| P | $\frac{1}{6}$ | $\frac{1}{4}$ | m | $\frac{1}{3}$ |
| A. | $\frac{7}{12}$ | B. | $\frac{1}{2}$ | C. | $\frac{5}{12}$ | D. | $\frac{1}{6}$ |
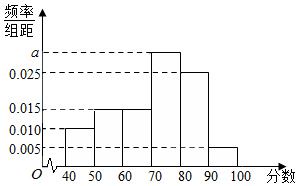 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成如下六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成如下六段:[40,50),[50,60),…,[90,100]后得到如图的频率分布直方图.