题目内容
18．已知一扇形的周长为24cm，当这个扇形的面积最大时，半径R的值为（ ）| A． | 4 cm | B． | 5cm | C． | 6cm | D． | 7cm |
分析 根据扇形的弧长与半径的关系，建立等式，再根据面积公式转化成关于R的二次函数，通过解二次函数最值求出结果．
解答 解：扇形的弧长为l=24-2R，
∴扇形的面积为S=$\frac{1}{2}$lR
=$\frac{1}{2}$（24-2R）•R=-R2+12R
=-（R-6）2+36，
∴当半径R=6cm时，扇形的面积最大．
故选：C．
点评 本题考查了函数模型的选择与应用问题，通过对实际问题的分析，抽象出数学模型，利用二次函数定义求解，是基础题目．
练习册系列答案
名校课堂系列答案
相关题目
8．设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的右焦点为F，点F到渐近线的距离为2a，则该双曲线的离心率等于（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\sqrt{5}$ | D． | 3 |
9．设命题p：函数f（x）=x2+ax+$\frac{1}{x}$在（$\frac{1}{2}$，+∞）上是增函数，命题q：a≥0，则p是q的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
6．在等比数列{an}中，a3，a15是方程x2-6x+8=0的根，则$\frac{{{a_1}{a_{17}}}}{a_9}$的值为（ ）
| A． | $2\sqrt{2}$ | B． | 4 | C． | $±2\sqrt{2}$ | D． | ±4 |
13．向量$\overrightarrow{O{Z_1}}$对应的复数是5-4i，向量$\overrightarrow{O{Z_2}}$对应的复数是-5+4i，则向量$\overrightarrow{{Z_1}{Z_2}}$对应的复数是（ ）
| A． | -10+8i | B． | 10-8i | C． | -8+10i | D． | 8+-10i |
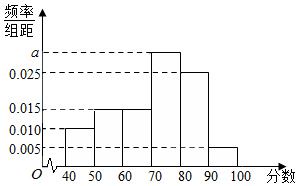某校从高一年级学生中随机抽取40名学生，将他们的期中考试数学成绩（满分100分，成绩均为不低于40分的整数）分成如下六段：[40，50），[50，60），…，[90，100]后得到如图的频率分布直方图．