题目内容
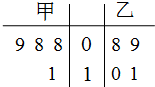甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示．（Ⅰ）分别计算甲、乙两名运动员训练得分的平均数和方差，并指出谁的训练成绩更好，为什么？
（Ⅱ）从甲、乙两名运动的训练成绩中各随机抽取1次的得分，分别记为x，y，设ξ=|x-8|+|y-10|．求ξ的分布列和数学期望．
考点：离散型随机变量的期望与方差,茎叶图
专题：概率与统计
分析：（Ⅰ）计算甲、乙两名运动员训练得分的平均数和方差，得到乙的平均水平比甲高，乙的训练成绩比甲稳定，乙的训练成绩更好些．
（Ⅱ）由题意知ξ=0，1，2，3，4，5，分别求出相应的概率，由此能求出ξ的分布列和数学期望．
（Ⅱ）由题意知ξ=0，1，2，3，4，5，分别求出相应的概率，由此能求出ξ的分布列和数学期望．
解答：
解：（Ⅰ）∵
=
(8+8+9+11)=9，
=
[(8-9)2×2+(9-9)2+(11-9)2]=
．…（2分）
=
(8+9+10+11)=
，
=
[(8-
)2+(9-
)2+(10-
)2+(11-
)2]=
．…（4分）
＜
，
＞
，
说明乙的平均水平比甲高，乙的训练成绩比甲稳定，
∴乙的训练成绩更好些．…（5分）
（Ⅱ）由题意知ξ=0，1，2，3，4，5，
P(ξ=0)=
=
，
P(ξ=1)=
=
，
P(ξ=2)=
=
，
P(ξ=3)=
=
，
P(ξ=4)=
=
，
P(ξ=5)=
=
，…（8分）
∴ξ的分布列为：
…（10分）
E(ξ)=0×
+1×
+2×
+3×
+4×
+5×
=2．…（12分）
. |
| x甲 |
| 1 |
| 4 |
| s | 2 甲 |
| 1 |
| 4 |
| 3 |
| 2 |
. |
| x乙 |
| 1 |
| 4 |
| 19 |
| 2 |
| s | 2 乙 |
| 1 |
| 4 |
| 19 |
| 2 |
| 19 |
| 2 |
| 19 |
| 2 |
| 19 |
| 2 |
| 5 |
| 4 |
. |
| x甲 |
. |
| x乙 |
| s | 2 甲 |
| s | 2 乙 |
说明乙的平均水平比甲高，乙的训练成绩比甲稳定，
∴乙的训练成绩更好些．…（5分）
（Ⅱ）由题意知ξ=0，1，2，3，4，5，
P(ξ=0)=
| ||||
|
| 1 |
| 8 |
P(ξ=1)=
| ||||||||
|
| 5 |
| 16 |
P(ξ=2)=
| ||||||||
|
| 1 |
| 4 |
P(ξ=3)=
| ||||||||
|
| 1 |
| 8 |
P(ξ=4)=
| ||||
|
| 1 |
| 8 |
P(ξ=5)=
| ||||
|
| 1 |
| 16 |
∴ξ的分布列为：
| ξ | 0 | 1 | 2 | 3 | 4 | 5 | ||||||||||||
| P |
|
|
|
|
|
|
E(ξ)=0×
| 1 |
| 8 |
| 5 |
| 16 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 16 |
点评：本题考查平均数、方差的求法，考查离散型随机变量的分布列和数学期望的求法，解题时要认真审题，是中档题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目