题目内容
已知函数f（x）=4cos2x-4
sinxcosx-2（x∈R）．
（1）求函数f（x）的单调递增区间；
（2）设△ABC的内角A，B，C对应边分别为a、b、c，且c=3，f（C）=-4，若向量
=（1，sinA）与向量
=（1，2sinB）共线，求a、b的值．
| 3 |
（1）求函数f（x）的单调递增区间；
（2）设△ABC的内角A，B，C对应边分别为a、b、c，且c=3，f（C）=-4，若向量
| m |
. |
| n |
考点：三角函数中的恒等变换应用,平面向量数量积的运算,正弦函数的图象
专题：解三角形
分析：（1）利用三角函数中的恒等变换应用可求得f（x）=4cos（2x+
），利用余弦函数的单调性即可求得函数f（x）的单调递增区间；
（2））f（C）=4cos（2C+
）=-4，结合题意易求C=
，再利用正弦定理与余弦定理即可求得a、b的值．
| π |
| 3 |
（2））f（C）=4cos（2C+
| π |
| 3 |
| π |
| 3 |
解答：
解：（1）f（x）=4cos2x-4
sinxcosx-2=2cos2x-2
sin2x
=4cos（2x+
）…3分
由2kπ+π≤2x+
≤2kπ+2π，（k∈Z）
解得：kπ+
≤x≤kπ+
，（k∈Z）…5分
∴f（x）的单调递增区间为[kπ+
，kπ+
]，（k∈Z）…6分
（2）f（C）=4cos（2C+
）=-4，而C∈（0，π），所以2C+
∈（
，
），
∴2C+
=π，得C=
…8分
∵
=（1，sinA）与向量
=（1，2sinB）共线，∴
=2，
由正弦定理得：
=2①…9分
由余弦定理得：c2=a2+b2-2abcos
，即a2+b2-ab=9②…11分
由①②解得a=2
，b=
…12分
| 3 |
| 3 |
=4cos（2x+
| π |
| 3 |
由2kπ+π≤2x+
| π |
| 3 |
解得：kπ+
| π |
| 3 |
| 5π |
| 6 |
∴f（x）的单调递增区间为[kπ+
| π |
| 3 |
| 5π |
| 6 |
（2）f（C）=4cos（2C+
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 7π |
| 3 |
∴2C+
| π |
| 3 |
| π |
| 3 |
∵
| m |
| n |
| sinA |
| sinB |
由正弦定理得：
| a |
| b |
由余弦定理得：c2=a2+b2-2abcos
| π |
| 3 |
由①②解得a=2
| 3 |
| 3 |
点评：本题考查三角函数中的恒等变换应用、平面向量数量积的运算、正弦定理与余弦定理，考查运算求解能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
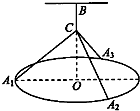如图，一个圆环O直径为4m，通过铁丝CA1，CA2，CA3，BC（A1，A2，A3是圆上三等分点）悬挂在B处，圆环呈水平状态，并距天花板2m，记四段铁丝总长为y（m）．
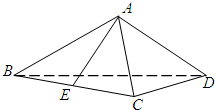如图，在体积为
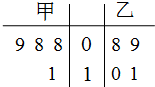甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示．
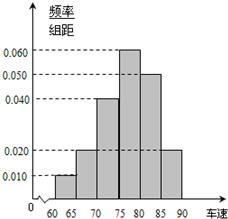某调查公司在某服务区调查七座以下小型汽车在某段高速公路的车速（km/t），办法是按汽车进服务区的先后每间隔50辆抽取一辆的抽样方法抽取40名驾驶员进行询问，将调查结果按[60，65）[65，70）[70，75）[75，80），[80，85）[85，90）分成六段，并得到如图所示的频率分布直方图．
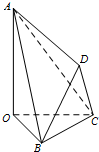如图，四面体OABC中，OA，OB，OC两两垂直，且OA=