题目内容
已知函数f(x)=xlnx.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)当k≤1时,求证:f(x)≥kx-1恒成立.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)当k≤1时,求证:f(x)≥kx-1恒成立.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)对f(x)求导,令f′(x)>0,得到单增区间;令f′(x)<0,得到单减区间.
(Ⅱ)可用两种方法证明之.
方法一:要证xlnx≥kx-1(x>0),即证lnx+
≥k,再令g(x)=lnx+
,x>0,再通过求导确定其最小值进行证明.
方法二:直接作差,令g(x)=f(x)-(kx-1)=xlnx-kx+1,依旧求导确定其性质从而进行证明.
(Ⅱ)可用两种方法证明之.
方法一:要证xlnx≥kx-1(x>0),即证lnx+
| 1 |
| x |
| 1 |
| x |
方法二:直接作差,令g(x)=f(x)-(kx-1)=xlnx-kx+1,依旧求导确定其性质从而进行证明.
解答:
解:
(Ⅰ) 定义域为(0,+∞),f′(x)=lnx+1,
令f′(x)=0,得 x=
,f′(x)与f(x)的情况如下:
所以f(x)的单调减区间为(0,
),单调增区间为(
,+∞)
(Ⅱ)方法一:要证xlnx≥kx-1(x>0),即证lnx+
≥k,
设g(x)=lnx+
,x>0,g′(x)=
-
=
,g'(x)与g(x)的情况如下:
所以g(x)≥g(1)=1,即lnx+
≥1在x>0时恒成立,
所以,当k≤1时,lnx+
≥k,
所以xlnx+1≥kx,即xlnx≥kx-1,
所以,当k≤1时,有f(x)≥kx.
方法二:令g(x)=f(x)-(kx-1)=xlnx-kx+1,g′(x)=lnx+1-k,
令g′(x)=0,得x=ek-1 ,
g′(x)与g(x)的情况如下:
g(x)的最小值为g(ek-1)=1-ek-1,
当k≤1时,ek-1≤1,所以1-ek-1≥0
故g(x)≥0.
即当k≤1时,f(x)≥kx-1.
(Ⅰ) 定义域为(0,+∞),f′(x)=lnx+1,
令f′(x)=0,得 x=
| 1 |
| e |
| x | (0,
|
|
(
| ||||||
| f′(x) | - | 0 | + | ||||||
| f(x) | ↘ | 极小值 | ↗ |
| 1 |
| e |
| 1 |
| e |
(Ⅱ)方法一:要证xlnx≥kx-1(x>0),即证lnx+
| 1 |
| x |
设g(x)=lnx+
| 1 |
| x |
| 1 |
| x |
| 1 |
| x2 |
| x-1 |
| x2 |
| x | (0,1) | 1 | (1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
| 1 |
| x |
所以,当k≤1时,lnx+
| 1 |
| x |
所以xlnx+1≥kx,即xlnx≥kx-1,
所以,当k≤1时,有f(x)≥kx.
方法二:令g(x)=f(x)-(kx-1)=xlnx-kx+1,g′(x)=lnx+1-k,
令g′(x)=0,得x=ek-1 ,
g′(x)与g(x)的情况如下:
| x | (0,ek-1) | ek-1 | (ek-1,+∞) |
| g′(x) | - | 0 | + |
| g(x) | ↘ | 极小值 | ↗ |
当k≤1时,ek-1≤1,所以1-ek-1≥0
故g(x)≥0.
即当k≤1时,f(x)≥kx-1.
点评:在证明不等式时,通过作差找到“差函数”,对“差函数”求导,从而确定其性质.当“差函数”形式比较复杂时,有时需要拆分“差函数”,分别进行研究,在这个过程中,参数分离也是常用的方法.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
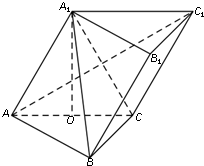 如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.
如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.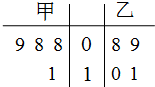 甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.
甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.