题目内容
已知函数f(x)=
cos2x+
sin2x+
,x∈R.
(1)求f(x)的最小正周期和最值;
(2)求函数f(x)的单调递增区间.
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
(1)求f(x)的最小正周期和最值;
(2)求函数f(x)的单调递增区间.
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)利用三角函数中的恒等变换应用可求得f(x)=sin(2x+
)+
,从而可求f(x)的最小正周期和最值;
(2)由(1)知f(x)=sin(2x+
)+
,利用正弦函数的单调性可求得函数f(x)的单调递增区间.
| π |
| 6 |
| 3 |
| 2 |
(2)由(1)知f(x)=sin(2x+
| π |
| 6 |
| 3 |
| 2 |
解答:
解:(1)f(x)=
cos2x+
sin2x+
=sin(2x+
)+
…(2分)
∴f(x)的最小正周期为T=
=π,最大值为
,最小值为
…(6分)
(2)由(1)知f(x)=sin(2x+
)+
,
故-
+2kπ≤2x+
≤
+2kπ(k∈Z)…(8分)
∴-
+kπ≤x≤
+kπ(k∈Z)…(10分)
故函数f(x)=sin(2x+
)+
的单调递增区间为[-
+kπ,
+kπ](k∈Z)…(12分)
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 2 |
=sin(2x+
| π |
| 6 |
| 3 |
| 2 |
∴f(x)的最小正周期为T=
| 2π |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
(2)由(1)知f(x)=sin(2x+
| π |
| 6 |
| 3 |
| 2 |
故-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
∴-
| π |
| 3 |
| π |
| 6 |
故函数f(x)=sin(2x+
| π |
| 6 |
| 3 |
| 2 |
| π |
| 3 |
| π |
| 6 |
点评:本题考查三角函数中的恒等变换应用,着重考查正弦函数的周期性、单调性及最值,属于中档题.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
圆心在直线l:x-y+1=0上,且过A(1,1),B(2,-2)两点的圆的方程为( )
| A、(x-3)2+(y-2)2=25 |
| B、(x+3)2+(y-2)2=25 |
| C、(x-3)2+(y+2)2=25 |
| D、(x+3)2+(y+2)2=25 |
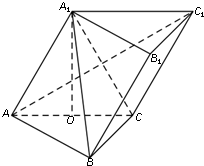 如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.
如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.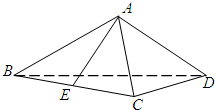 如图,在体积为
如图,在体积为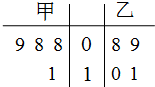 甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.
甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.