题目内容
函数f(x)=-x2+4(0≤x≤2)的图象与坐标轴围成的平面区域记为M,满足不等式组
的平面区域记为N,已知向区域M内任意地投掷一个点,落入区域N的概率为
,则a的值为 .
|
| 3 |
| 32 |
考点:几何概型,简单线性规划
专题:概率与统计
分析:根据概率公式求出平面区域N的面积,利用线性规划的知识即可得到结论.
解答:
解:由积分的几何意义可知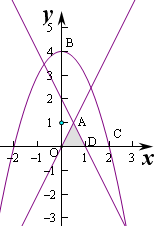 平面区域记为M的面积S=
平面区域记为M的面积S=
(-x2+4)dx=(-
x3+4x)|
=
,
平面区域N的图形为△OAD,
已知向区域M内任意地投掷一个点,落入区域N的概率为
,
则
=
,
即S△OAD=
,
∵D(1,0),
∴S△OAD=
=
×1×yA,
则yA=1,此时xA=
,即A(
,1),
同时A也在直线2x+ay-2=0上,代入得2×
+a-2=0,
解得a=1,
故答案为:1
 平面区域记为M的面积S=
平面区域记为M的面积S=| ∫ | 2 0 |
| 1 |
| 3 |
2 0 |
| 16 |
| 3 |
平面区域N的图形为△OAD,
已知向区域M内任意地投掷一个点,落入区域N的概率为
| 3 |
| 32 |
则
| S△OAD | ||
|
| 3 |
| 32 |
即S△OAD=
| 1 |
| 2 |
∵D(1,0),
∴S△OAD=
| 1 |
| 2 |
| 1 |
| 2 |
则yA=1,此时xA=
| 1 |
| 2 |
| 1 |
| 2 |
同时A也在直线2x+ay-2=0上,代入得2×
| 1 |
| 2 |
解得a=1,
故答案为:1
点评:本题主要考查几何概型的应用以及利用积分求区域面积,综合性较强,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
二次函数f(x)=ax2+2a是区间[-a,a2]上的偶函数,又g(x)=f(x-1),则g(0),g(
),g(3)的大小关系是( )
| 3 |
| 2 |
A、g(
| ||
B、g(0)<g(
| ||
C、g(
| ||
D、g(3)<g(
|
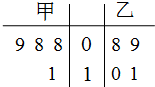 甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.
甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.
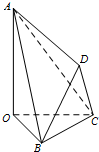 如图,四面体OABC中,OA,OB,OC两两垂直,且OA=
如图,四面体OABC中,OA,OB,OC两两垂直,且OA=