题目内容
已知函数f(x)=2cos2x+
sin2x,g(x)=
f(x+
)+ax+b,其中a,b为非零实常数.
(1)若f(α)=1-
,α∈[-
,
],求α的值
(2)若x∈R,讨论g(x)的奇偶性,并证明你的结论
(3)已知对任意x1,x2∈R,恒有|sinx1-sinx2|≤|x1-x2|,当且仅当x1=x2时等号成立,若g(x)是上R的增函数,根据上述结论,求a的取值范围.
| 3 |
| 1 |
| 2 |
| 5π |
| 12 |
(1)若f(α)=1-
| 3 |
| π |
| 3 |
| π |
| 3 |
(2)若x∈R,讨论g(x)的奇偶性,并证明你的结论
(3)已知对任意x1,x2∈R,恒有|sinx1-sinx2|≤|x1-x2|,当且仅当x1=x2时等号成立,若g(x)是上R的增函数,根据上述结论,求a的取值范围.
考点:三角函数中的恒等变换应用,函数奇偶性的判断
专题:三角函数的图像与性质
分析:(1)利用两角和公式和二倍角公式对函数解析式化简,利用α范围和函数解析式求得α的值.
(2)根据f(x)的范围确定g(x)的范围,对b=-
时和;b≠-
时分类讨论.
(3)设x1<x2,表示出g(x2)-g(x1)根据函数的单调性,判断出g(x2)-g(x1)>0,推断出a>
,进而根据|
|<
=2求得a范围.
(2)根据f(x)的范围确定g(x)的范围,对b=-
| 1 |
| 2 |
| 1 |
| 2 |
(3)设x1<x2,表示出g(x2)-g(x1)根据函数的单调性,判断出g(x2)-g(x1)>0,推断出a>
| sin2x2-sin2x1 |
| x2-x1 |
| sin2x2-sin2x1 |
| x2-x1 |
| |2x2-2x1| |
| x2-x1 |
解答:
解:(1)f(x)=2cos2x+
sin2x=cos2x+
sin2x+1=2sin(2x+
)+1,
∴f(α)=2sin(2α+
)+1=1-
,
sin(2α+
)=-
,
∵α∈[-
,
],
∴2α+
∈[-
,
],
∴2α+
=-
,
∴α=-
(2)g(x)=-sin2x+ax+b+
,
所以b=-
时,g(x)为奇函数;b≠-
时,g(x)为非奇非偶函数.
(3)设x1<x2,则g(x2)-g(x1)=sin2x1-sin2x2+a(x2-x1)
因为,g(x)是R上的增函数,所以g(x2)-g(x1)=sin2x1-sin2x2+a(x2-x1)>0恒成立
又x2-x1>0,
∴a>
恒成立,
又∵|
|=2•|
|≤2,
∴a≥2.
| 3 |
| 3 |
| π |
| 6 |
∴f(α)=2sin(2α+
| π |
| 6 |
| 3 |
sin(2α+
| π |
| 6 |
| ||
| 2 |
∵α∈[-
| π |
| 3 |
| π |
| 3 |
∴2α+
| π |
| 6 |
| π |
| 2 |
| 5π |
| 6 |
∴2α+
| π |
| 6 |
| π |
| 3 |
∴α=-
| π |
| 4 |
(2)g(x)=-sin2x+ax+b+
| 1 |
| 2 |
所以b=-
| 1 |
| 2 |
| 1 |
| 2 |
(3)设x1<x2,则g(x2)-g(x1)=sin2x1-sin2x2+a(x2-x1)
因为,g(x)是R上的增函数,所以g(x2)-g(x1)=sin2x1-sin2x2+a(x2-x1)>0恒成立
又x2-x1>0,
∴a>
| sin2x2-sin2x1 |
| x2-x1 |
又∵|
| sin2x2-sin2x1 |
| x2-x1 |
| sin2x2-sin2x1 |
| 2x2-2x1 |
∴a≥2.
点评:本题主要考查了三角函数恒等变换的应用,函数的单调性和奇偶性.考查了学生分析问题和推理的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列的通项公式an=2n-37,则Sn取最小值时n=( )
| A、18 | B、19 |
| C、18或19 | D、20 |
在数列{an}中,a1=1,an+2+(-1)nan=2,记Sn为数列{an}的前项和,则S61=( )
| A、931 | B、961 |
| C、991 | D、1021 |
圆心在直线l:x-y+1=0上,且过A(1,1),B(2,-2)两点的圆的方程为( )
| A、(x-3)2+(y-2)2=25 |
| B、(x+3)2+(y-2)2=25 |
| C、(x-3)2+(y+2)2=25 |
| D、(x+3)2+(y+2)2=25 |
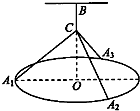 如图,一个圆环O直径为4m,通过铁丝CA1,CA2,CA3,BC(A1,A2,A3是圆上三等分点)悬挂在B处,圆环呈水平状态,并距天花板2m,记四段铁丝总长为y(m).
如图,一个圆环O直径为4m,通过铁丝CA1,CA2,CA3,BC(A1,A2,A3是圆上三等分点)悬挂在B处,圆环呈水平状态,并距天花板2m,记四段铁丝总长为y(m).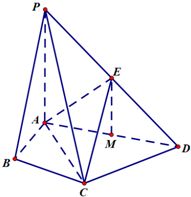 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,M为AD的中点,PA=2AB=4.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,M为AD的中点,PA=2AB=4.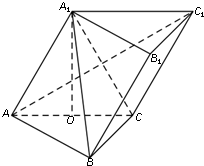 如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.
如图,在斜三棱柱ABC-A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.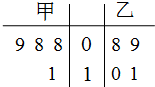 甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.
甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示.