题目内容
在△ABC中，角A，B，C所对的边分别为a，b，c，已知S△ABC=
accosB．
（Ⅰ）求角B的大小；
（Ⅱ）b=2
，a=2，求c．
| ||
| 2 |
（Ⅰ）求角B的大小；
（Ⅱ）b=2
| 2 |
考点：正弦定理,余弦定理
专题：解三角形
分析：（Ⅰ）利用面积公式和已知等式求得tanB的值，进而求得B．
（Ⅱ）根据（Ⅰ）求得B的值，和余弦定理求得关于c的一元二次方程，进而求得c．
（Ⅱ）根据（Ⅰ）求得B的值，和余弦定理求得关于c的一元二次方程，进而求得c．
解答：
解：（Ⅰ）由已知得
acsinB=
cacosB，
∴tanB=
，
∵0＜B＜π，
∴B=
．
（Ⅱ）由余弦定理得b2=a2+c2-2accosB，
∴8=4+c2-2ac×
，即c2-2c-4=0，
∴c=1±
，
∵c＞0，
∴c=1+
．
| 1 |
| 2 |
| ||
| 2 |
∴tanB=
| 3 |
∵0＜B＜π，
∴B=
| π |
| 3 |
（Ⅱ）由余弦定理得b2=a2+c2-2accosB，
∴8=4+c2-2ac×
| 1 |
| 2 |
∴c=1±
| 5 |
∵c＞0，
∴c=1+
| 5 |
点评：本题主要考查了正弦定理和余弦定理的应用．注重了对学生基础知识的考查．
练习册系列答案
相关题目
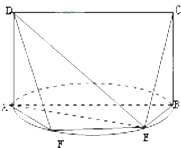如图，E是以AB为直径的半圆上异于点A、B的点，矩形ABCD所在的平面垂直于该半圆所在平面，且AB=2AD=2．
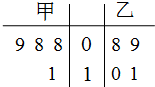甲、乙两名运动员在4次训练中的得分情况如下面的茎叶图所示．
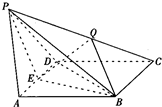已知四棱锥P-ABCD中，底面ABCD是菱形，AB=PA=PD=2，∠ABD=