Question

如图，PA、PB切⊙O于A，B两点，CD切⊙O于点E，交PA，PB于C、D，若⊙O的半径为r，△PCD的周长等于3r，则tan∠APB的值是（　　）

• A、

  12

  5

• B、

  12

  5

  13

• C、

  3

  5

  13

• D、

  2

  3

  13

Answer 1

考点：弦切角

专题：三角函数的求值,立体几何

分析：连接OA，OB，OP，延长BO交PA的延长线于点F，利用切线长定理可得CA=CE，DB=DE，PA=PB，再由△PCD的周长等于3r，可得PA=PB=

3

2

r，进而求出∠APO的三角函数值，最后利用二倍角公式得到答案．

解答： 解：连接OA，OB，OP，如图所示：

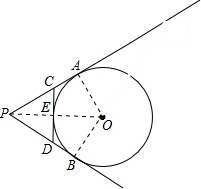
由切线长定理可得CA=CE，DB=DE，PA=PB，
故PC+CD+PD=PA+PB=2PA=3r，
∴PA=PB=

3

2

r，
故tan∠APO=

r

3 2 r

=

2

3

，
故tan∠APB=tan2∠APO=

2tan∠APO

1-tan2∠APO

=

4 3

1-( 2 3 )2

=

4 3

5 9

=

12

5

，
故选：A

点评：本题考查的知识点是切线长定理，二倍角的正切公式，是三角函数与平面几何的综合应用，难度中档．