题目内容
若函数f（x）=loga（a-x）在[2，3]上单调递减，则a的取值范围是 ．
考点：对数函数的图像与性质
专题：函数的性质及应用
分析：根据复合函数的单调性的条件判断
求解即可．
|
解答：
解：∵函数f（x）=loga（a-x）在[2，3]上单调递减，u（x）=a-x在[2，3]上单调递减，
∴
，解得a＞3
故答案为：a＞3，
∴
|
故答案为：a＞3，
点评：本题考查了函数的性质，复合函数的单调性的求解，注意定义域的限制，属于中档题．
练习册系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
如图，PA、PB切⊙O于A，B两点，CD切⊙O于点E，交PA，PB于C、D，若⊙O的半径为r，△PCD的周长等于3r，则tan∠APB的值是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
①正相关，②负相关，③不相关，则下列散点图分别反映的变量是（ ）
| A、①②③ | B、②③① |
| C、②①③ | D、①③② |
已知函数f（x）=
，则函数f（x）的零点为（ ）
|
A、
| ||
| B、-2，0 | ||
C、C、
| ||
| D、0 |
函数y=
sinx(
＜x＜
)的值域是（ ）
| 1 |
| 2 |
| π |
| 6 |
| π |
| 2 |
A、（0，
| ||||
B、(
| ||||
C、(0，
| ||||
| D、（0，1） |
已知在区间[-1，1]上随机地取一个数x，则-π（x2-1）的值介于
到π之间的概率为（ ）
| 8π |
| 9 |
A、
| ||
B、
| ||
C、
| ||
D、
|
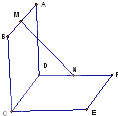如图，已知两个正方形ABCD 和DCEF不在同一平面内，M，N分别为AB，DF的中点．若平面ABCD⊥平面DCEF，求直线MN与平面DCEF所成角的正弦值．