Question

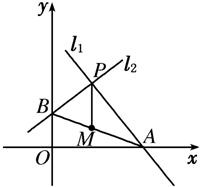
过P（1，3）作两互相垂直的直线l₁和l₂，l₁交x轴于点A，l₂与y轴交于点B，求线段AB中点M的轨迹方程．

Answer 1

考点：轨迹方程

专题：综合题,直线与圆

分析：设M的坐标为（x，y），欲求线段AB的中点M的轨迹方程，只须求出坐标x，y的关系式即可，由题意得2|PM|=|AB|，利用两点间的距离公式将点的坐标代入后化简即得M的轨迹方程．

解答： 解：设M的坐标为（x，y），
则A、B两点的坐标分别是（2x，0），（0，2y），连接PM，
∵l₁⊥l₂，∴2|PM|=|AB|．
而|PM|=

(x-1)2+(y-3)2

，
|AB|=

(2x)2+(2y)2

，
∴2

(x-1)2+(y-3)2

=

(2x)2+(2y)2

．
化简，得x+3y-5=0即为所求的轨迹方程．

点评：本题主要考查了轨迹方程、两条直线垂直等知识，属于中档题．