题目内容
(1)已知函数f(x)=|x-2|+|2x+1|,若不等式|2m+3|+|m-3|≥|m|•f(x)对任意m∈R且m≠0恒成立,求x的取值范围.
(2)对于x∈R,不等式|x-1|+|x-2|≥a2+b2+c2恒成立,试求a+2b+3c的最大值.
(2)对于x∈R,不等式|x-1|+|x-2|≥a2+b2+c2恒成立,试求a+2b+3c的最大值.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)依题意,得g(x)≤
对任意m∈R且m≠0恒成立,利用绝对值三角不等式易求|2m+3|+|m-3|≥|3m|,于是可得g(x)≤3,解不等式:|x-2|+|2x+1|≤3即可;
(2)利用绝对值三角不等式易求|x-1|+|x-2|=|x-1|+|2-x|≥|x-1+2-x|=1,于是得a2+b2+c2≤1,利用柯西不等式(a+2b+3c)2≤(12+22+32)( a2+b2+c2)≤14,即可得到答案.
| |2m+3|+|m-3| |
| |m| |
(2)利用绝对值三角不等式易求|x-1|+|x-2|=|x-1|+|2-x|≥|x-1+2-x|=1,于是得a2+b2+c2≤1,利用柯西不等式(a+2b+3c)2≤(12+22+32)( a2+b2+c2)≤14,即可得到答案.
解答:
解:(1)不等式|2m+3|+|m-3|≥|m|•g(x)对任意m∈R且m≠0恒成立转化为g(x)≤
对任意m∈R且m≠0恒成立.…(2分)
因为|2m+3|+|m-3|≥|3m|⇒
≥3所以g(x)≤3…(4分)
所以解不等式:|x-2|+|2x+1|≤3
,或
,或
…(6分)
得x∈[-
,0]…(7分)
(2)|x-1|+|x-2|=|x-1|+|2-x|≥|x-1+2-x|=1,…(9分)
当且仅当(x-1)(2-x)≥0取等号,故a2+b2+c2≤1.…(10分)
由柯西不等式(a+2b+3c)2≤(12+22+32)( a2+b2+c2)≤14.…(12分)
由
⇒
,
即取a=
,b=
,c=
时等号成立.
故(a+2b+3)max=
.…(14分)
| |2m+3|+|m-3| |
| |m| |
因为|2m+3|+|m-3|≥|3m|⇒
| |2m+3|+|m-3| |
| |m| |
所以解不等式:|x-2|+|2x+1|≤3
|
|
|
得x∈[-
| 2 |
| 3 |
(2)|x-1|+|x-2|=|x-1|+|2-x|≥|x-1+2-x|=1,…(9分)
当且仅当(x-1)(2-x)≥0取等号,故a2+b2+c2≤1.…(10分)
由柯西不等式(a+2b+3c)2≤(12+22+32)( a2+b2+c2)≤14.…(12分)
由
|
|
即取a=
| ||
| 14 |
| ||
| 7 |
3
| ||
| 14 |
故(a+2b+3)max=
| 14 |
点评:本题考查绝对值三角不等式与柯西不等式的应用,突出考查等价转化思想与综合运算求解能力,属于难题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图,在五棱锥S-ABCDE中,SA⊥底面ABCDES,SA=AB=AE=2,BC=DE=
如图,在五棱锥S-ABCDE中,SA⊥底面ABCDES,SA=AB=AE=2,BC=DE=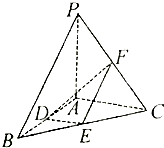 如图,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,D、E、F分别是棱AB、BC、CP的中点,AB=AC=1,PA=2.
如图,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,D、E、F分别是棱AB、BC、CP的中点,AB=AC=1,PA=2.