题目内容
已知实数x,y,满足xy=1,且x>2y>0,则
的最小值为 .
| x2+4y2 |
| x-2y |
考点:基本不等式
专题:不等式的解法及应用
分析:根据分式中分母的特征,将分子配方,即可拆成基本不等式的形式,从而获得最小值.
解答:
解:∵xy=1,且x>2y>0,
∴
=
=(x-2y)+
≥2
=4.
当且仅当x-2y=
即x-2y=2时,取“=”号,
此时,联立xy=1,得
时,
有最小值4.
故答案为:4.
∴
| x2+4y2 |
| x-2y |
| (x-2y)2+4xy |
| x-2y |
| 4 |
| x-2y |
(x-2y)•
|
当且仅当x-2y=
| 4 |
| x-2y |
此时,联立xy=1,得
|
| x2+4y2 |
| x-2y |
故答案为:4.
点评:1.解决本题的突破口是:平方、拆项,化为基本不等式的形式.应学会一些常见的变形技巧.
2.利用基本不等式时,应注意是否满足条件“一正,二定,三相等”,否则取不到最值.
2.利用基本不等式时,应注意是否满足条件“一正,二定,三相等”,否则取不到最值.

练习册系列答案
相关题目
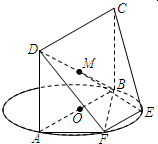 如图,AB为圆O的直径,点E,F在圆上,四边形ABCD为矩形,AB∥EF,∠BAF=
如图,AB为圆O的直径,点E,F在圆上,四边形ABCD为矩形,AB∥EF,∠BAF=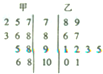 某科考试中,从甲、乙两个班级各随机抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
某科考试中,从甲、乙两个班级各随机抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.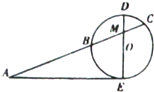 如图,AE切圆O于点E,AC交圆O于B,C两点,且与直径DE交于点M,DM=2,CM=3,BM=6,则tanA=
如图,AE切圆O于点E,AC交圆O于B,C两点,且与直径DE交于点M,DM=2,CM=3,BM=6,则tanA=