题目内容
 圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线C1:
圆x2+y2=4的切线与x轴正半轴,y轴正半轴围成一个三角形,当该三角形面积最小时,切点为P(如图),双曲线C1:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
(Ⅰ)求C1的方程;
(Ⅱ)若椭圆C2过点P且与C1有相同的焦点,直线l过C2的右焦点且与C2交于A,B两点,若以线段AB为直径的圆过点P,求l的方程.
考点:直线与圆锥曲线的关系,双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)设切点P(x0,y0),(x0>0,y0>0),利用相互垂直的直线斜率之间的关系可得切线的斜率和切线的方程,即可得出三角形的面积,利用基本不等式的性质可得点P的坐标,再利用双曲线的标准方程及其性质即可得出;
(Ⅱ)由(Ⅰ)可得椭圆C2的焦点.可设椭圆C2的方程为
+
=1(b1>0).把P的坐标代入即可得出方程.由题意可设直线l的方程为x=my+
,
A(x1,y1),B(x2,y2),与椭圆的方程联立即可得出根与系数的关系,再利用向量垂直与数量积的关系即可得出.
(Ⅱ)由(Ⅰ)可得椭圆C2的焦点.可设椭圆C2的方程为
| x2 | ||
3+
|
| y2 | ||
|
| 3 |
A(x1,y1),B(x2,y2),与椭圆的方程联立即可得出根与系数的关系,再利用向量垂直与数量积的关系即可得出.
解答:
解:(Ⅰ)设切点P(x0,y0),(x0>0,y0>0),则切线的斜率为-
,
可得切线的方程为y-y0=-
(x-x0),化为x0x+y0y=4.
令x=0,可得y=
;令y=0,可得x=
.
∴切线与x轴正半轴,y轴正半轴围成一个三角形的面积S=
•
•
=
.
∵4=
+
≥2x0y0,当且仅当x0=y0=
时取等号.
∴S≥
=4.此时P(
,
).
由题意可得
-
=1,e=
=
=
,解得a2=1,b2=2.
故双曲线C1的方程为x2-
=1.
(Ⅱ)由(Ⅰ)可知双曲线C1的焦点(±
,0),即为椭圆C2的焦点.
可设椭圆C2的方程为
+
=1(b1>0).
把P(
,
)代入可得
+
=1,解得
=3,
因此椭圆C2的方程为
+
=1.
由题意可设直线l的方程为x=my+
,A(x1,y1),B(x2,y2),
联立
,化为(m2+2)y2+2
my-3=0,
∴y1+y2=-
,y1y2=
.
∴x1+x2=m(y1+y2)+2
=
,
x1x2=m2y1y2+
m(y1+y2)+3=
.
=(
-x1,
-y1),
=(
-x2,
-y2),
∵
⊥
,∴
•
=0,
∴x1x2-
(x1+x2)+y1y2-
(y1+y2)+4=0,
∴2m2-2
m+4
-11=0,解得m=
-1或m=-(
-1),
因此直线l的方程为:x-(
-1)y-
=0或x+(
-1)y-
=0.
| x0 |
| y0 |
可得切线的方程为y-y0=-
| x0 |
| y0 |
令x=0,可得y=
| 4 |
| y0 |
| 4 |
| x0 |
∴切线与x轴正半轴,y轴正半轴围成一个三角形的面积S=
| 1 |
| 2 |
| 4 |
| y0 |
| 4 |
| x0 |
| 8 |
| x0y0 |
∵4=
| x | 2 0 |
| y | 2 0 |
| 2 |
∴S≥
| 8 |
| 2 |
| 2 |
| 2 |
由题意可得
| 2 |
| a2 |
| 2 |
| b2 |
| c |
| a |
1+
|
| 3 |
故双曲线C1的方程为x2-
| y2 |
| 2 |
(Ⅱ)由(Ⅰ)可知双曲线C1的焦点(±
| 3 |
可设椭圆C2的方程为
| x2 | ||
3+
|
| y2 | ||
|
把P(
| 2 |
| 2 |
| 2 | ||
3+
|
| 2 | ||
|
| b | 2 1 |
因此椭圆C2的方程为
| x2 |
| 6 |
| y2 |
| 3 |
由题意可设直线l的方程为x=my+
| 3 |
联立
|
| 3 |
∴y1+y2=-
2
| ||
| 2+m2 |
| -3 |
| 2+m2 |
∴x1+x2=m(y1+y2)+2
| 3 |
4
| ||
| m2+2 |
x1x2=m2y1y2+
| 3 |
| 6-6m2 |
| m2+2 |
| AP |
| 2 |
| 2 |
| BP |
| 2 |
| 2 |
∵
| AP |
| BP |
| AP |
| BP |
∴x1x2-
| 2 |
| 2 |
∴2m2-2
| 6 |
| 6 |
3
| ||
| 2 |
| ||
| 2 |
因此直线l的方程为:x-(
3
| ||
| 2 |
| 3 |
| ||
| 2 |
| 3 |
点评:本题综合考查了圆锥曲线的标准方程及其性质、相互垂直的直线斜率之间的关系、向量垂直与数量积的关系、切线的斜率和切线的方程、三角形的面积计算公式、基本不等式的性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系等基础知识与基本技能方法,考查了推理能力和计算能力,考查了转化和化归能力,考查了解决问题的能力,属于难题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
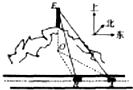 如图,一辆汽车在一条水平的公路上向正西方向行驶,在A处分别测得山顶上铁塔的塔顶E的仰角为θ和山脚点O(点O是点E在公路所在平面上的射影)的方位角是西偏北φ,再行驶akm到达B处,测得山脚点O的方位角是西偏北β.请设计一个方案,用测量的数据和有关公式写出计算OE的步骤.
如图,一辆汽车在一条水平的公路上向正西方向行驶,在A处分别测得山顶上铁塔的塔顶E的仰角为θ和山脚点O(点O是点E在公路所在平面上的射影)的方位角是西偏北φ,再行驶akm到达B处,测得山脚点O的方位角是西偏北β.请设计一个方案,用测量的数据和有关公式写出计算OE的步骤.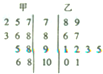 某科考试中,从甲、乙两个班级各随机抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.
某科考试中,从甲、乙两个班级各随机抽取10名同学的成绩进行统计分析,两班成绩的茎叶图如图所示,成绩不小于90分为及格.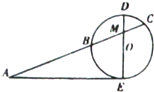 如图,AE切圆O于点E,AC交圆O于B,C两点,且与直径DE交于点M,DM=2,CM=3,BM=6,则tanA=
如图,AE切圆O于点E,AC交圆O于B,C两点,且与直径DE交于点M,DM=2,CM=3,BM=6,则tanA=