题目内容
14.已知集合A={x||x-2|≤1},B={x|x2-2mx+m2-4≤0,m∈R}(1)若A∩B=[2,3],求实数m的值;
(2)若A⊆∁RB,求实数m的取值范围.
分析 (1)解绝对值不等式和一元二次不等式化简集合A,B,然后利用集合端点值的关系列式求解;
(2)求出B的补集,由A⊆∁RB,利用两集合端点值之间的关系列式求解.
解答 解:A={x||x-2|≤1}={x|1≤x≤3},
B={x|x2-2mx+m2-4≤0,m∈R}={x|m-2≤x≤m+2}.
(1)∵A∩B=[2,3],∴$\left\{\begin{array}{l}{m-2=2}\\{m+2≥3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m=4}\\{m≥1}\end{array}\right.$.
∴m=4;
(2)∁RB={x|x<m-2或x>m+2},
∵A⊆∁RB,∴m-2>3或m+2<1.
解得m<-1或m>5.
点评 本题考查了交集及其运算,考查了补集及其运算,训练了二次不等式的解法,是基础题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.如图是正方体的平面展开图,则在这个正方体中,AM与BN所成角的大小为( )


| A. | 0° | B. | 45° | C. | 60° | D. | 90° |
2.设函数f(x)=$\left\{{\begin{array}{l}{{2^x},x≤0}\\{{{log}_3}x,x>0}\end{array}}$,则$f({f({\frac{1}{9}})})$的值是( )
| A. | $\frac{1}{4}$ | B. | 4 | C. | $\frac{1}{9}$log32 | D. | -4 |
2.在△ABC所在平面上有一点P,满足$\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=2\overrightarrow{AB}$,则△APC与△ABC的面积比为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
 的左、右焦点分别为
的左、右焦点分别为 ,椭圆
,椭圆 过点
过点 ,直线
,直线 交
交 轴于
轴于 ,且
,且 ,
,  为坐标原点.
为坐标原点.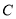 的方程;
的方程;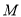 是椭圆
是椭圆 的上顶点,过点
的上顶点,过点 分别作直线
分别作直线 交椭圆
交椭圆 于
于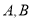 两点,设这两条直线的斜率分别为
两点,设这两条直线的斜率分别为 ,且
,且 ,证明:直线
,证明:直线 过定点.
过定点.