设函数f(x)=$\left\{{\begin{array}{l}{{2^x}.x≤0}\\{{{log} 3}x.x＞0}\end{array}}$.则$f$的值是( )A．$\frac{1}{4}$B．4C．$\frac{1}{9}$log32D．-4 题目和参考答案——青夏教育精英家教网—

题目内容

2．设函数f（x）=$\left\{{\begin{array}{l}{{2^x}，x≤0}\\{{{log}_3}x，x＞0}\end{array}}$，则$f（{f（{\frac{1}{9}}）}）$的值是（　　）

A．

$\frac{1}{4}$

B．

C．

$\frac{1}{9}$log₃2

D．

-4

分析先求出f（$\frac{1}{9}$）=$lo{g}_{3}\frac{1}{9}$=-2，从而$f（{f（{\frac{1}{9}}）}）$=f（-2），由此能求出结果．

解答解：∵函数f（x）=$\left\{{\begin{array}{l}{{2^x}，x≤0}\\{{{log}_3}x，x＞0}\end{array}}$，
∴f（$\frac{1}{9}$）=$lo{g}_{3}\frac{1}{9}$=-2，
$f（{f（{\frac{1}{9}}）}）$=f（-2）=2^-2=$\frac{1}{4}$．
故选：A．

点评本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．

练习册系列答案

13．函数f（x）=a^x-1-2（a＞0，a≠1）的图象恒过定点A，若点A在直线mx-ny-1=0上，其中m＞0，n＞0，则$\frac{1}{m}$+$\frac{2}{n}$的最小值为（　　）

10．若（1-2x）²⁰¹⁷=a₀+a₁x+a₂x²+…+a₂₀₁₇x²⁰¹⁷（x∈R），则$\frac{1}{2}$a₁+$\frac{1}{{2}^{2}}$a₂+$\frac{1}{{2}^{3}}$a₃+…+$\frac{1}{{2}^{2017}}$a₂₀₁₇的值为-1．

17．

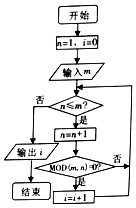已知MOD函数是一个求余函数，MOD（m，n）表示m除以n的余数，例如MOD（8，3）=2，如图是某个算法的程序框图，若输入m的值为6，则输出i的值为（　　）

7．命题“?x∈[1，2]，x²-2x-a≤0”为真命题的一个充分不必要条件是（　　）

14．已知集合A={x||x-2|≤1}，B={x|x²-2mx+m²-4≤0，m∈R}
（1）若A∩B=[2，3]，求实数m的值；
（2）若A⊆∁_RB，求实数m的取值范围．

10．在△ABC中，若a=2$\sqrt{3}，cosC=\frac{1}{3}，{S_{△ABC}}=4\sqrt{3}$，则b=3$\sqrt{2}$．

11．已知函数f（x）是定义在R上的奇函数，且图象连续不断，对任意0＜x₁＜x₂，有$\frac{{f（{x_1}）-f（{x_2}）}}{{{x_1}-{x_2}}}＞-1$，且f（2）=1，则不等式-3≤f（x）+x≤0的解集为[-2，0]．

试题分类