题目内容
9.已知集合A={x||x-2|≤1},B={x|x2-2tx+t2-4≤0,t∈R}(1)若A∩B=[2,3],求实数t的取值范围;
(2)若A⊆∁RB,求实数t的取值范围.
分析 (1)运用绝对值不等式和二次不等式的解法,化简集合A,B,由交集的定义,即可得到t的范围;
(2)求出∁RB,由A⊆∁RB,可得t的不等式,解不等式即可得到t的范围.
解答 解:(1)集合A={x||x-2|≤1}={x|1≤x≤3}=[1,3],
B={x|x2-2tx+t2-4≤0,t∈R}={x|t-2≤x≤t+2}=[t-2,t+2],
若A∩B=[2,3],则t-2=2,即t=4,B=[2,6],符合要求.
则t=4,即t的取值范围是{4};
(2)∁RB={x|x>t+2或x<t-2},
由A⊆∁RB,可得t-2>3或t+2<1,
解得t>5或t<-1.
可得t的取值范围是(5,+∞)∪(-∞,-1).
点评 本题考查集合的交集和集合的包含关系,考查二次不等式和绝对值不等式的解法,运用定义法是解题的关键,属于中档题.

练习册系列答案
相关题目
19.已知函数f(x)=x2+(2a-1)x+1,若对区间(2,+∞)内的任意两个不等实数x1,x2都有$\frac{f({x}_{1}-1)-f({x}_{2}-1)}{{x}_{1}-{x}_{2}}$>0,则实数a的取值范围是( )
| A. | (-∞,-$\frac{1}{2}$] | B. | [-$\frac{5}{2}$,+∞) | C. | [-$\frac{1}{2}$,+∞) | D. | (-∞,$-\frac{5}{2}$] |
18.设函数f(x)是定义在R上的奇函数,且f(1)=0,当x>0时,f′(x)-f(x)<0恒成立,则不等式ln|x|f(x)>0的解集为( )
| A. | {x|-1<x<0或x<-1} | B. | {x|-1<x<0或x>1} | C. | {x|x<-1或0<x<1} | D. | {x|-1<x<0或0<x<1} |
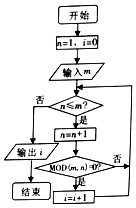 已知MOD函数是一个求余函数,MOD(m,n)表示m除以n的余数,例如MOD(8,3)=2,如图是某个算法的程序框图,若输入m的值为6,则输出i的值为( )
已知MOD函数是一个求余函数,MOD(m,n)表示m除以n的余数,例如MOD(8,3)=2,如图是某个算法的程序框图,若输入m的值为6,则输出i的值为( ) 执行程序框图,如果输入x=9时,输出y=$\frac{29}{9}$,则整数a值为1.
执行程序框图,如果输入x=9时,输出y=$\frac{29}{9}$,则整数a值为1.