题目内容
5.在△ABC中,已知 $sinA+cosA=\frac{1}{5}$.(1)判断△ABC是锐角还是钝角三角形;
(2)求tanA.
分析 (1)把$sinA+cosA=\frac{1}{5}$两边平方,得1+2sinA•cosA=$\frac{1}{25}$,从而sinA•cosA=-$\frac{12}{25}$.进而A为钝角,由此得到△ABC是钝角三角形.
(2)由sinA•cosA=-$\frac{12}{25}$,sin2A+cos2A=1,求出sinA=$\frac{4}{5}$,cosA=-$\frac{3}{5}$,由此能求出tanA.
解答 解:(1)在△ABC中,∵$sinA+cosA=\frac{1}{5}$,
∴两边平方可得1+2sinA•cosA=$\frac{1}{25}$,
∴sinA•cosA=-$\frac{12}{25}$.
∵0<A<π,∴A为钝角,∴△ABC是钝角三角形.
(2)∵sinA•cosA=-$\frac{12}{25}$,
又sin2A+cos2A=1,
∴sinA=$\frac{4}{5}$,cosA=-$\frac{3}{5}$,
∴tanA=$\frac{sinA}{cosA}$=-$\frac{4}{3}$.
点评 本题考查三角形形状的判断,考查三角形的角的正切值的求法,考查同角三角函数关系式、三角形性质等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
16.已知X~N(5,1),若P(5<X≤6)=0.3413,P(3<X≤7)=0.9544,则P(6<X≤7)=( )
| A. | 0.3413 | B. | 0.4772 | C. | 0.8185 | D. | 0.1359 |
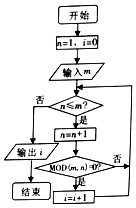 已知MOD函数是一个求余函数,MOD(m,n)表示m除以n的余数,例如MOD(8,3)=2,如图是某个算法的程序框图,若输入m的值为6,则输出i的值为( )
已知MOD函数是一个求余函数,MOD(m,n)表示m除以n的余数,例如MOD(8,3)=2,如图是某个算法的程序框图,若输入m的值为6,则输出i的值为( ) 执行程序框图,如果输入x=9时,输出y=$\frac{29}{9}$,则整数a值为1.
执行程序框图,如果输入x=9时,输出y=$\frac{29}{9}$,则整数a值为1. ,设
,设 ,且
,且 ,则
,则 的最小值为( )
的最小值为( ) B.
B.  C.
C.  D.
D. 