题目内容
13.在△ABC中,内角A,B,C的对边分别是a,b,c,且$a=bcosC+\frac{{\sqrt{3}}}{3}csinB$.(1)求角B的值;
(2)若a+c=6,且△ABC的面积为$\frac{{3\sqrt{3}}}{2}$,求边b的长.
分析 (1)利用已知条件通过正弦定理以及两角和的正弦函数求解得到sinC,然后求解B的正确函数值.
(2)利用三角形的面积求出ab的值,然后通过余弦定理,转化求解.
解答 解:(1)由$a=bcosC+\frac{{\sqrt{3}}}{3}$csinB及正弦定理得:$sinA=sinBcosC+\frac{{\sqrt{3}}}{3}sinCsinB$.…(1分)
∴$sin({B+C})=sinBcosC+\frac{{\sqrt{3}}}{3}sinCsinB$.…(2分)
∴$sinBcosC+cosBsinC=sinBcosC+\frac{{\sqrt{3}}}{3}sinCsinB$.…(3分)
∴$cosBsinC=\frac{{\sqrt{3}}}{3}sinCsinB$…(4分)
又∵C为三角形内角,可得sinC≠0,
∴$tanB=\sqrt{3}$.…(5分)
∵B∈(0,π),
∴$B=\frac{π}{3}$.…(6分)
(2)∵△ABC面积为$\frac{{3\sqrt{3}}}{2}$,∴$\frac{1}{2}acsinB=\frac{{3\sqrt{3}}}{2}$,即$\frac{1}{2}ac•\frac{{\sqrt{3}}}{2}=\frac{{3\sqrt{3}}}{2}$,ac=6.…(9分)
由余弦定理得,b2=a2+c2-2accosB=(a+c)2-3ac=36-18=18,
∴$b=3\sqrt{2}$.…(12分)
点评 本题考查正弦定理以及余弦定理的应用,考查三角形的面积以及三角形的解法,考查计算能力.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
4.函数y=(3-x2)ex的单调递增区间是( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,-3) | D. | (-3,1) |
1.某一算法框图如图,输出的S值为( )
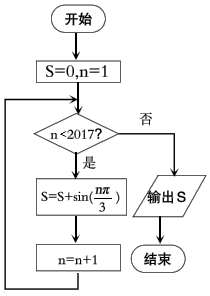

| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | 0 |
8.已知函数f(x)=m(x+m+3)(x+m+2),g(x)=2x-2,若?x∈R,f(x)<0或g(x)<0恒成立,则实数m的取值范围为( )
| A. | (-3,0) | B. | (-2,0) | C. | (-3,-2) | D. | (0,3) |
18.双曲线$\frac{x^2}{2}-\frac{y^2}{4}=1$渐近线的斜率为( )
| A. | $±\frac{{\sqrt{2}}}{2}$ | B. | $±\frac{1}{2}$ | C. | $±\sqrt{2}$ | D. | ±2 |
5.若函数f(x)=x2ex-a恰有三个零点,则实数a的取值范围是( )
| A. | $({\frac{4}{e^2},+∞})$ | B. | $({0,\frac{4}{e^2}})$ | C. | (0,4e2) | D. | (0,+∞) |