题目内容
18.双曲线$\frac{x^2}{2}-\frac{y^2}{4}=1$渐近线的斜率为( )| A. | $±\frac{{\sqrt{2}}}{2}$ | B. | $±\frac{1}{2}$ | C. | $±\sqrt{2}$ | D. | ±2 |
分析 求出双曲线的渐近线方程,然后推出结果.
解答 解:双曲线$\frac{x^2}{2}-\frac{y^2}{4}=1$渐近线方程为:y=$±\sqrt{2}$x,
双曲线$\frac{x^2}{2}-\frac{y^2}{4}=1$渐近线的斜率为:$±\sqrt{2}$.
故选:C.
点评 本题考查双曲线的简单性质的应用,是基础题.

练习册系列答案
相关题目
8.如图,给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2016}$的值的程序框图,其中判断框内可填入的是( )
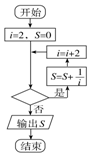

| A. | i≤2 021? | B. | i≤2 019? | C. | i≤2 017? | D. | i≤2 015? |
6.已知变量x,y满足约束条件$\left\{\begin{array}{l}x+y-1≥0\\ x-1≤0\\ 3x-y+1≥0\end{array}\right.$,则目标函数z=x+y的最小值为( )
| A. | 5 | B. | 3 | C. | 1 | D. | 0 |
3.已知数列{an}是递增等差数列,且a1+a4=5,a2a3=6,设${b_n}=\frac{1}{{{a_n}•{a_{n+1}}}}$,则数列{bn}的前10项和为( )
| A. | $\frac{9}{10}$ | B. | $\frac{11}{10}$ | C. | $\frac{9}{11}$ | D. | $\frac{10}{11}$ |
10.命题“?x∈R,使得x2+x+1>0”的否定是( )
| A. | ?x0∈R,使得x02+x0+1>0 | B. | ?x∈R,使得x2+x+1>0 | ||
| C. | ?x∈R,使得x2+x+1≤0 | D. | ?x0∈R,使得x02+x0+1≤0 |