题目内容
1.某一算法框图如图,输出的S值为( )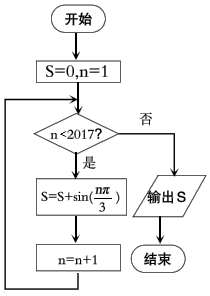
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | 0 |
分析 由已知中的程序框图可知:该程序的功能是利用循环结构计算并输出变量S的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
解答 解:由已知中的程序框图可知:
该程序的功能是利用循环结构计算并输出变量S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sinπ+…+sin$\frac{2016π}{3}$的值,
由于y=sin$\frac{nπ}{3}$的周期为6,且同一周期内各函数值的累加和为0,
由于2016÷6=336,
故S=sin$\frac{π}{3}$+sin$\frac{2π}{3}$+sinπ+…+sin$\frac{2016π}{3}$=336×0=0,
故选:D.
点评 本题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法解答,属于基础题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
16.已知函数f(x)=-x5-3x3-5x+3,若f(a)+f(a-2)>6,则实数a的取值范围是( )
| A. | (-∞,3) | B. | (3,+∞) | C. | (1,+∞) | D. | (-∞,1) |
6.已知变量x,y满足约束条件$\left\{\begin{array}{l}x+y-1≥0\\ x-1≤0\\ 3x-y+1≥0\end{array}\right.$,则目标函数z=x+y的最小值为( )
| A. | 5 | B. | 3 | C. | 1 | D. | 0 |
10.命题“?x∈R,使得x2+x+1>0”的否定是( )
| A. | ?x0∈R,使得x02+x0+1>0 | B. | ?x∈R,使得x2+x+1>0 | ||
| C. | ?x∈R,使得x2+x+1≤0 | D. | ?x0∈R,使得x02+x0+1≤0 |
11.已知平面向量$\overrightarrow a$,$\overrightarrow b$满足$\overrightarrow a$($\overrightarrow a$+$\overrightarrow b$)=5,且|$\overrightarrow a$|=2,|$\overrightarrow b$|=1,则向量$\overrightarrow a$与$\overrightarrow b$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |