题目内容
3.若函数f(x)=ax2-(2a+1)x+a+1对于任意a∈[-1,1],都有f(x)<0,则实数x的取值范围是(1,2).分析 把原函数整理成关于a的一次函数,利用一次函数的单调性求得函数在[-1,1]上的最大值,令最大值小于0,可得x的范围.
解答 解:函数可整理为f(x)=(x2-x+1)a+1-x
∵对于a∈[-1,1]时恒有f(x)<0,
∴(x2-x+1)a+1-x<0恒成立.
令g(a)=(x2-2x+1)a+1-x.
则函数g(a)在区间[-1,1]上的最大值小于0,
∵g(a)为一次函数,且一次项系数x2-2x+1>0,
∴函数g(a)在区间[-1,1]上单调递增,
∴g(a)max=g(1)=x2-2x+1+1-x=x2-3x+2<0.
解得1<x<2.
故答案为:(1,2).
点评 本题主要考查了利用函数的单调性求函数最大值.在把恒成立问题转化为求函数的最值问题的过程中,体现了转化的思想.

练习册系列答案
相关题目
14. 考拉兹猜想又名3n+1猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图所示的程序框图,运行相应程序,输出的结果i=( )
考拉兹猜想又名3n+1猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图所示的程序框图,运行相应程序,输出的结果i=( )
 考拉兹猜想又名3n+1猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图所示的程序框图,运行相应程序,输出的结果i=( )
考拉兹猜想又名3n+1猜想,是指对于每一个正整数,如果它是奇数,则对它乘3再加1;如果它是偶数,则对它除以2.如此循环,最终都能得到1.阅读如图所示的程序框图,运行相应程序,输出的结果i=( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
18.设f(x)是R上的奇函数f(x+4)=f(x),当x∈[0,1]时,f(x)=3x,则f(11.5)=( )
| A. | 1.5 | B. | 0.5 | C. | -1.5 | D. | -0.5 |
8.如图,给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2016}$的值的程序框图,其中判断框内可填入的是( )
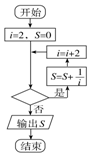

| A. | i≤2 021? | B. | i≤2 019? | C. | i≤2 017? | D. | i≤2 015? |